Задача 55232 ...
Условие
Линия задана уравнением ρ = ρ(ϕ) в полярной системе координат. Требуется:
1) построить линию по точкам, придавая ϕ значения через промежуток
π/4;
2) найти уравнение кривой в прямоугольной системе координат, начало которой совмещено с полюсом, а положительная полуось Ox – с полярной осью.
ρ = 3(1 + 2 sin ϕ).
Решение
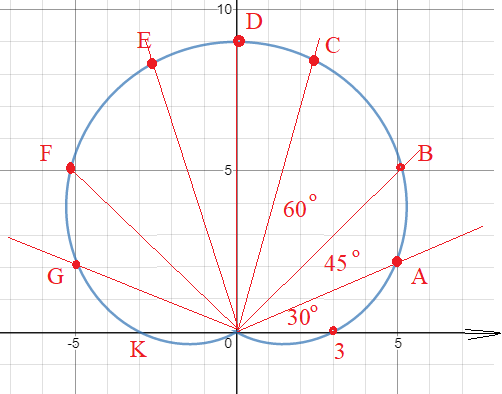
( см. рис.)
Луч вращается на 360 ^(o) и заполняет всю координатную плоскость
хОу
Координатами в полярной системе координат являются угол φ и расстояние r
Расстояние r≥ 0
φ =0^(o) ⇒ r=3*(1+2*sin0^(o))=3*(1+2*0)=3*1=3
Откладываем отрезок длины 3 на луче в 0^(o)
φ =30^(o) ⇒ r=3*(1+2*sin30^(o))=3*(1+1)=6
Откладываем отрезок длины 6 на луче в 30^(o)
Получаем точку A
φ =45^(o) ⇒ r=3*(1+2*sin45^(o))≈3*(1+1,4)=7,2
Откладываем отрезок длины 7,2 на луче в 45^(o)
Получаем точку B
φ =60^(o) ⇒ r=3*(1+2*sin60^(o))≈3*(1+1,7)=8,1
Откладываем отрезок длины 8,1 на луче в 60^(o)
Получаем точку C
φ =90^(o) ⇒ r=3*(1+2*sin 90^(o))=3*(1+2)=3*3=9
Откладываем отрезок длины 9 на луче в 90^(o)
Получаем точку D
и так далле
φ =120^(o) ⇒
φ =135^(o) ⇒
φ =150^(o) ⇒
φ =180^(o) ⇒
и так далее до 360 градусов
2)
Переход от полярных к декартовым.
Декартовы через полярные:
x= ρ *cos φ
y= ρ *sin φ ⇒
Полярные через декартовы:
sin φ=y/ ρ
x^2+y^2=( ρ *cos φ)^2+( ρ *sin φ)^2= ρ ^2*(cos^2 φ +sin^2 φ )= ρ ^2*1 ⇒ ρ =sqrt(x^2+y^2)
ρ = 3(1 + 2 sin ϕ) ⇒ [b]sqrt(x^2+y^2)=3*1+6*(y/sqrt(x^2+y^2)) [/b]⇒ упростить