Задача 35798 ...

sova

2019-04-13 14:15:13

Построить кривую, заданную в полярных координатах
r=3,5*(1-cos φ )

Полярная система координат задается точкой отсчета О и лучом
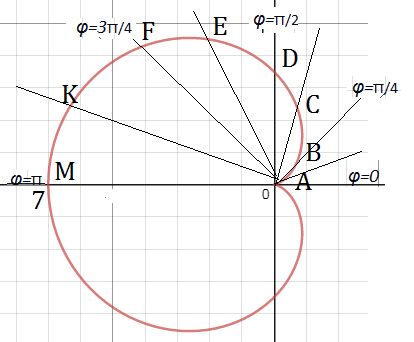
( см. рис.)
Луч вращается на 360 ^(o) и заполняет всю координатную плоскость
хОу
Координатами в полярной системе координат являются угол φ и расстояние r

Расстояние r≥ 0

φ =0^(o) ⇒ r=3,5(1-cos0^(o))=0

φ =30^(o) ⇒ r=3,5(1-cos30^(o))≈(7/2)*(1-(1,7)/2)=0,502
Откладываем отрезок длины 0,502 на луче в 30^(o)
Получаем точку А

φ =45^(o) ⇒ r=3,5(1-cos45^(o))≈(7/2)*(2-1,4)/2=1,05
Откладываем отрезок длины 1,05 на луче в 45^(o)
Получаем точку B

φ =60^(o) ⇒ r=3,5(1-cos60^(o))=3,5*(1-0,5)=7/4=1,75
Откладываем отрезок длины 1,75 на луче в 60^(o)
Получаем точку C

φ =90^(o) ⇒ r=3,5(1-cos90^(o))=3,5*(1-0)=3,5
Откладываем отрезок длины 3,5 на луче в 90^(o)
Получаем точку D

φ =120^(o) ⇒ r=3,5(1-cos120^(o))=3,5*(1-(-0,5))=7/4=5,25
Откладываем отрезок длины 5,25 на луче в 120^(o)
Получаем точку E

φ =135^(o) ⇒ r=3,5(1-cos135^(o))≈(7/2)*(2+1,4)/2=5,95
Откладываем отрезок длины 5,95 на луче в 135^(o)
Получаем точку F

φ =150^(o) ⇒ r=3,5(1-cos150^(o))≈(7/2)*(2+1,7)/2=6,5
Откладываем отрезок длины 6,5 на луче в 150^(o)
Получаем точку K

φ =180^(o) ⇒ r=3,5(1-cos180^(o))≈(7/2)*(1-(-1))=7
Откладываем отрезок длины 7 на луче в 180^(o)
Получаем точку M

и так далее до 360 градусов или 2π радиан