Задача 66216 Найти уравнение кривой (х^2 + у^2)^2...

63417ca0c2a19543dc25a6c0

14.10.2022 14:47:03

Найти уравнение кривой (х^2 + у^2)^2 =2у^2 в полярной системе координат. Построить кривую.

5f3ea7e3faf909182968ddd9

14.10.2022 16:18:17

★

x= ρ cos θ

y= ρ sin θ

x^2+y^2= ρ ^2cos^2 θ + ρ ^2sin^2 θ= ρ ^2*(cos^2 θ +sin^2 θ )= ρ ^2*1= ρ ^2


Уравнение принимает вид:

(ρ ^2)^2=2*ρ^2 sin^2 θ ⇒

ρ ^4=2*ρ^2 sin^2 θ ⇒

ρ ^2=2sin^2 θ

[b] ρ =sqrt(2)sin θ [/b]

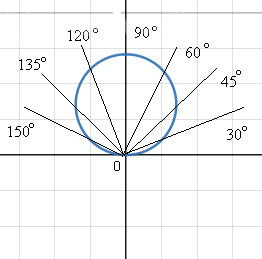
θ =30 ° ⇒ ρ =sqrt(2)*(1/2) [/b]

(30 ° ; sqrt(2)/2)

θ =45 ° ⇒ ρ =sqrt(2)*(sqrt(2)/2) [/b]

(45 ° ; 1)

θ =60 ° ⇒ ρ =sqrt(2)*(sqrt(3)/2) [/b]

(60 ° ; sqrt(6)/2)

и так далее