Задача 62535 Перейти в уравнение кривой к полярным...
Условие

Решение
y = ρ · sinφ
x^2+y^2=(ρ · cosφ )^2+(ρ · sinφ)^2=ρ^2 · cos^2φ+ρ^2 · sin^2φ=ρ^2 · (cos^2φ+ sin^2φ)=ρ^2 · 1=ρ^2
Подставляем в данное уравнение
(x²+y²)³ = 8yx ^(9) не понятно какой там показатель степени
(ρ²)³ =8( ρ · sinφ) ( ρ ·cosφ)^(9)
Упрощаем:
ρ^6 =8ρ^(10) · sinφ · (cosφ)^(9) ⇒
1=8ρ^(4) · sinφ · (cosφ)^(9) ⇒
ρ^(4) =[m]\frac{1}{sin φ cos^9 φ }[/m] это уж очень сложно.
Поэтому думаю, что там 3
(ρ²)³ =8( ρ · sinφ) ( ρ ·cosφ)^(3)
Упрощаем:
ρ^6 =8ρ^(4) · sinφ · (cosφ)^(3) ⇒
ρ^2=8 · sinφ · (cosφ)^(3) ⇒ ρ^2 =4sin2 φ *cos^2 φ
[m]ρ =2cos φ \sqrt{sin2 φ }[/m] - это лучше.
[m]sin2 φ ≥ 0[/m] ⇒
2πn ≤ 2 φ ≤ π+2πn, n ∈ [b]Z[/b]
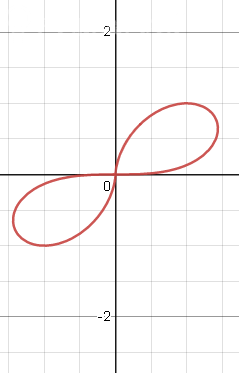
πn ≤ φ ≤ (π/2)+πn, n ∈ [b]Z[/b] ⇒ график состоит из двух одинаковых "лепестков" в первой и третьей четвертях
Строим первый:
φ =15 ° ⇒ [m]ρ =2cos15 ° \sqrt{sin30 ° } ≈ [/m]
проводим луч под углом 15 ° и откладываем найденное значение ρ
φ =30 ° ⇒ [m]ρ =2cos30 ° \sqrt{sin60 ° } ≈ [/m]
проводим луч под углом 30 ° и откладываем найденное значение ρ
и так далее
см. рисунок