Задача 62493 Линия задана уравнением r = r(фи) в...
Условие
Требуется:
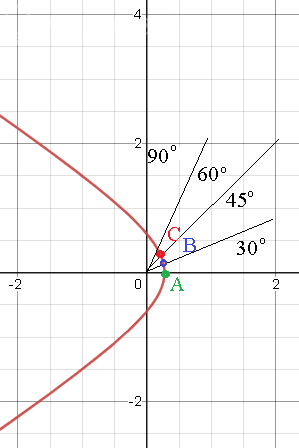
1) построить линию по точкам от фи=0 до фи =пи , придавая значения через промежуток пи/6;
2) найти уравнение линии в декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось OX - с
полярной осью;
3) определить вид линии по уравнению в декартовой системе координат;
4) сделать чертеж.
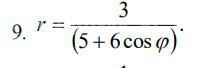
Решение
В полярной системе координат используется [b]полярный луч[/b]
Любой луч задается точкой отсчета и направлением.
Направление полярного луча - положительное.
Поэтому на нем откладываем отрезки, значения которыx больше или равны 0
ρ ≥ 0 ⇒ 3 /(5+6cosφ)≥0 ⇒ 5+6cosφ≥0 ⇒ cosφ≥-5/6
Решив это тригонометрическое неравенство получим ограничения на полярный угол.
В данной задаче полярный угол :
-(arccos(-5/6) ≤ φ ≤ arccos (-5/6)
(φ=180 ° не берем!)
1)
[b]φ =0[/b]⇒ сos0=1
ρ=3/(5+6*1)=3/11≈0,27
На луче φ =0 откладываем расстояние ρ=3/11
получаем точку [b]А (0;3/11)[/b]
[b]φ =π/6[/b]⇒сosπ/6=sqrt(3)/2 ≈ 0,87
ρ=3/(5+6*0,87)=0,3
На луче φ =π/6 откладываем расстояние ρ=0,3
получаем точку[b] В (π/6; 0,3)[/b]
[b]φ =π/4[/b]⇒cos(π/4)=sqrt(2)/2 ≈0,7
ρ=3/(5+6*0,7)≈0,32
На луче φ =π/4 откладываем расстояние ρ≈0,32
получаем точку[b] С (π/4;0,32)[/b]
[b]φ =π/3[/b]⇒cos(π/3)=1/2
ρ=3/(5+6*(1/2))=0,375
На луче φ =π/6 откладываем расстояние ρ=0,375
получаем точку[b] D (π/3;0,375)[/b]
[b]φ =π/2[/b]⇒cos(π/2)=0
ρ=3/(5+6*0)=3/5=0,6
На луче φ =π/2 откладываем расстояние ρ=0,375
получаем точку[b] F (π/2;0,6)[/b]
и так далее
2) найти уравнение линии в декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось OX – с
полярной осью
x= ρ cos φ
y= ρ sin φ
[red]ρ =3/(5+6cos φ )[/red]
ρ=sqrt((x^2+y^2))
cos φ =x/sqrt((x^2+y^2))
Тогда уравнение примет вид
[red]sqrt((x^2+y^2))=3/(5+6x/sqrt((x^2+y^2)) )[/red] ⇒
[b]5sqrt(x^2+y^2)+6x=3[/b] ⇒
25(x^2+y^2)=(3-6x)^2
25x^2+25y^2=9-36x+36x^2
11x^2-36x-25y^2+9=0
можно выделить полный квадрат
3) определить вид линии по уравнению в декартовой системе координат
11x^2-36x-25y^2+9=0 - уравнение гиперболы со смещенным центром
вида
(x-x_(o))^2/a^2 + (y^2/b^2)=1