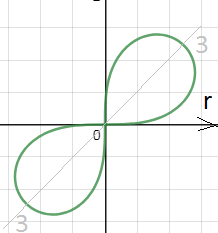Задача 31184 ...

dashokkkk

21 ноября 2018 г. в 13:00

а) построить по точкам в полярной системе координат кривые (r ≥ 0)

б) перейдя к полярной системе координат, построить кривые.

а) r = 3sin2φ

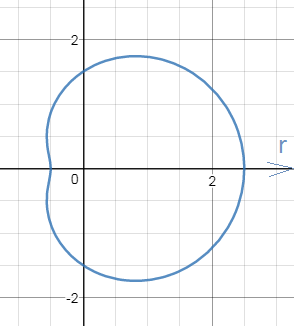
б) 4(x²+y²–x)² = 9(x²+y²)

sova

21 ноября 2018 г. в 13:53

★

a
r ≥ 0 ⇒ sin2 φ ≥ 0 ⇒ 0+2πk ≤ 2 φ ≤ π+2πk, k ∈ Z ⇒
[b] πk ≤ φ ≤ (π/2)+πk, k ∈ Z ⇒
график расположен в 1 и 3 координатных углах плоскости.
см. рис. 1

б)
Вводим полярные координаты
x=r·cos φ
y=r·sin φ
x²+ y²=r²
так как cos² φ +sin² φ =1

Уравнение кривой принимает вид:
4(r²–r·sinφ)²=9·r²

4r²·(r–sin φ )²=9r²

(r–sin φ )²=9/4

см. рис. 2