Задача 57295 ...
Условие
1) построить линию по точкам, придавая ϕ значения через промежуток
π/4;
2) найти уравнение кривой в прямоугольной системе координат, начало которой совмещено с полюсом, а положительная полуось Ox – с полярной осью
Решение
Любой луч задается точкой отсчета и направлением.
Направление полярного луча - положительное.
Поэтому на нем откладываем отрезки, значения которыx ≥ 0
ρ ≥ 0 ⇒ cosφ - sinφ ≥ 0
Решив это тригонометрическое неравенство получим ограничения на полярный угол.
В данной задаче полярный угол от -135° ≤ φ ≤45°
1)
φ =5 °⇒ ρ =cos 5°-sin 5 °≈считаем
проводим луч под углом 5°; на нем откладываем длину ρ = cos 5°-sin 5 °≈
φ =10 °⇒ ρ =cos 10°-sin 10 °≈считаем
проводим луч под углом 10°; на нем откладываем длину
ρ = cos 10°-sin 10 °≈
φ =15 ° ⇒ ρ =cos 15°-sin 15 °≈ 0,9659-0,2588=0,7071
проводим луч под углом 15°; на нем откладываем длину ρ = cos 15°-sin 15 °≈0,7071
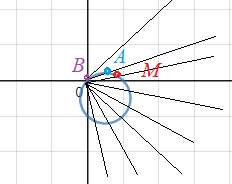
получаем точку M (15 ° ;≈0,7) Она изображена на рисунке.
φ =30 ° ⇒ ρ=cos 30°-sin 30 °=(sqrt(3)-1)/2
точка A (30 ° ;(sqrt(3)-1)/2)
φ =45 ° ⇒ ρ =cos 45°-sin 45 ° =0
точка B (45 ° ;0)
...
и
далее:
углы от 0 до -135° :
φ =-5 °⇒ ρ =cos (-5°)-sin(- 5 °)=cos (5°)+sin( 5 °)≈
φ =-10 °⇒ ρ =cos (-10°)-sin(- 10 °)=cos (10°)+sin( 10 °)≈
φ =15 ° ⇒ ρ =cos(- 15°)-sin (-15 °)=cos( 15°)+sin (15 °)≈ 0, 9659+0,2588
строим точку (-15 ° ;≈0, 9659+0,2588)
φ =30 ° ⇒ ρ=cos(- 30°)-sin(- 30 °)=cos( 30°)+sin( 30 °)=(sqrt(3)+1)/2
точка (-30 ° ;(sqrt(3)+1)/2)
φ =45 ° ⇒ ρ =cos 45°+sin 45 ° =sqrt(2)
точка (-45 ° ;sqrt(2))
2)
x= ρ cos φ ⇒ cos φ =x/ ρ
y= ρ sin φ ⇒ sin φ =y/ ρ
x^2+y^2= ρ ^2cos^2 φ + ρ sin^2 φ ⇒
x^2+y^2= ρ ^2
ρ =x/ ρ -y/ ρ ⇒ ρ ^2=x-y
x^2+y^2=x-y - уравнение в декартовой системе координат.
Упростим: выделим полные квадраты:
(x^2-x)+(y^2+y)=0
(x-0,5)^2+(y+0,5)^2=0,5
уравнение окружности с центром (0,5;-0,5) и радиусом R=sqrt(0,5)=sqrt(2)/2