Задача 31542 Перейти в уравнение кривой к полярным...
Условие
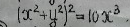
предмет не задан ВУЗ
2878
Решение
★
y=r*sin φ
x^2+y^2=r^2
Подставляем в данное уравнение:
(r^2)^2=10r^3cos^3 φ
r=10cos^3 φ
cos^3φ >0 в четвертой и первой четвертях
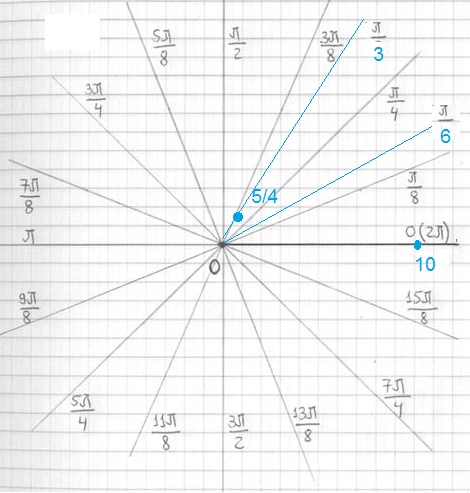
φ =-π/2⇒ r=10*0^3=0 Откладываем на луче -π/2 0, т. е получаем точку (0;0) на плоскости
φ =-π/3⇒ r=10*(1/2)^3=10/8=5/4
φ =-π/4⇒ r=10*(1/2sqrt(2))≈
φ =-π/6⇒ r=10*(3sqrt(3)/8)≈
φ =0⇒ r=10*1=10 Точка (10;0) на плоскости хОу
φ =π/6⇒ r=10*(3sqrt(3)/8)≈
φ =π/4⇒ r=10*(1/2sqrt(2))≈
φ =π/3⇒ r=10*(1/2)^3=10/8=5/4
φ =π/2⇒ r=0*0^3=0
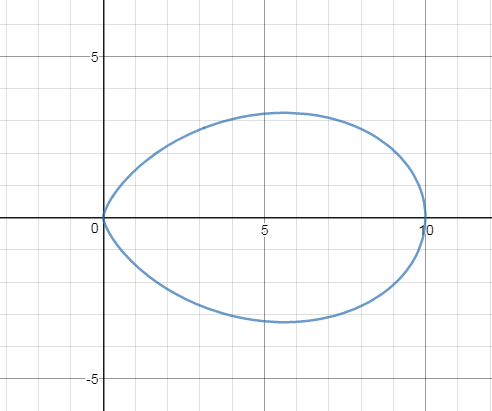
График см рис.