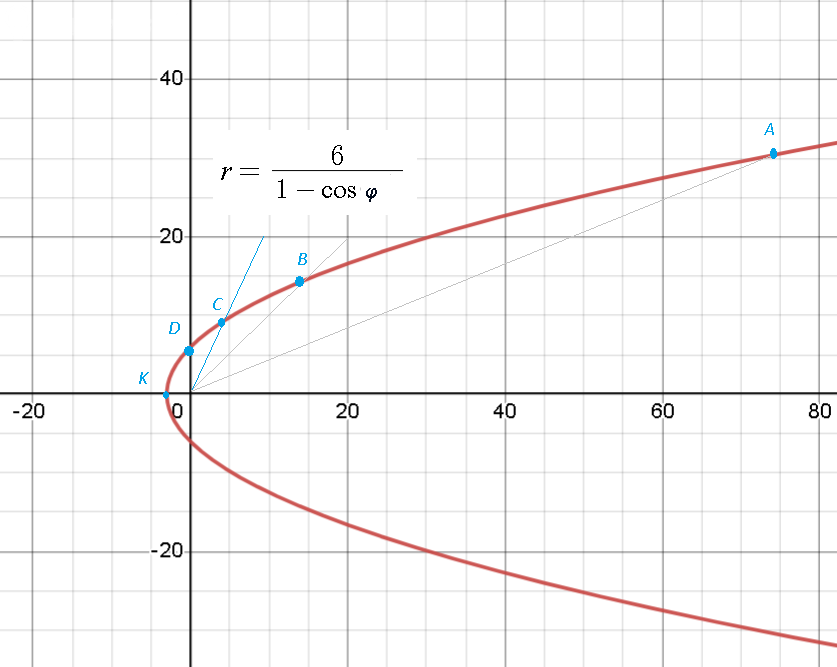
Задача 76070 ...
Условие
Даны уравнения линий в полярной системе координат.
Вар. 4.2. r = 6/(1–cosφ)
Требуется:
1) Построить линию на промежутке от φ=0 до φ=2π с шагом, равным π/8.
2) Найти уравнение линии в прямоугольной декартовой системе координат и назвать линию.
Решение
r=6/(1-cosφ)
(знаменатель дроби не должен равняться 0)
дроби обращается в 0
1-cosφ ≠ 0
cosφ ≠ 1
φ ≠ 0
При
φ =π/8⇒ cos(π/8)=0,92
ρ=6/(1-0,92)=6/0,08=75
На луче φ =π/8 откладываем расстояние ρ=75
получаем точку А(π/8; 75)
φ =π/4⇒cos (π/4)=sqrt(2)/2 ≈0,7
ρ≈6/(1-0,7)=6/0,3=20
На луче φ =π/4 откладываем расстояние ρ=20
получаем точку B (π/4;20)
φ =3π/8⇒cos (3π/8) ≈0,38
ρ≈6/(1-0,38)=6/0,62≈9,7
а луче φ =3π/8 откладываем расстояние ρ≈≈9,7
получаем точку C (3π/8;9,7)
φ =π/2⇒cos (π/2)=0
ρ=6/(1-0)=6
На луче φ =π/2 откладываем расстояние ρ=6
получаем точку D (π/2;6)
и так далее
φ =5π/8⇒
ρ=
φ =3π/4⇒cos(3π/4)=-sqrt(2)/2 ≈-0,7
ρ≈ 6/(1-(-0,7))=6/1,7=
На луче φ =3π/4 откладываем расстояние ρ≈
получаем точку G (3π/4;)
φ =7π/8⇒cos(7π/8) ≈-0,92
ρ≈ 6/(1-(-0,92))=6/1,92=
На луче φ =7π/8 откладываем расстояние ρ≈
φ =π⇒ cosπ=-1
ρ = 6/(1-(-1))=3
На луче φ =π откладываем расстояние ρ=3
получаем точку К (π; 3)
и так далее
Переход от полярной системы координат к декартовой
x=ρ·cos φ
y=ρ·sin φ
x^2+y^2=ρ^2⇒ ρ=sqrt(x^2+y^2)
cosφ =x/ρ=x/sqrt(x^2+y^2)
Подставляем в данное уравнение:
[m]\sqrt{x^2+y^2}=\frac{6}{1- \frac{x}{\sqrt{x^2+y^2}}}[/m]
Упрощаем
[m]\sqrt{x^2+y^2}-x=6[/m]
[m]\sqrt{x^2+y^2}=6+y[/m]
Возводим в квадрат
[m]x^2+y^2=36+12x+x^2[/m]
[m]y^2=36+12x[/m] - парабола