Практика (59)
Найдите все значения a, при которых уравнение a^2 - ax - 2x^2 - 0,5x - 2a + |a + 2,5x| = 0 имеет ровно три различных корня.

найти все значения x при каждом из которых неравенство (2-a)*x^3+(1-2a)*x^2-6x+(5+4a-a^2)<0 выполняется хотя бы при одном значении a, принадлежащем отрезку [-1;2]

Найдите все значения параметра a, при которых уравнение a|x-1|+(x^2-7x+12):(3-x)=0 имеет ровно одно решение
ЕГЭ -17 задание на параметры. Решить графическим способом
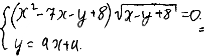
Найти значения а при которых неравенство(х^2 - 4х -а^4 + 4а^2)√(х^2-7х) ≤ 0 имеет 4 решения Решить надо.
Найти при каких значениях параметра a данная система уранений имеет 2 решения.

Найти все значения параметра a, при которых уравнение имеет единственное решение на отрезке [0; p].
p=9.
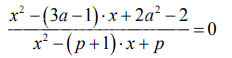
Найти все значения параметра a , при которых уравнение (a+4x+x^(2)-1)(a+9-1-|x-9|)=0 имеет ровно три различных решения.
p=9.
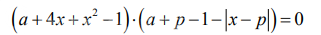
При каких значениях p вершины парабол [m]y=x²-10px-3[/m] и [m]y=x²+2px-5p[/m] расположены в одной полуплоскости относительно оси абсцисс.
Найти наибольшее целое значение параметра a, при котором уравнение √(a−2xу)=y−x+2 не имеет решений.
Найдите значение параметра φ, при котором система имеет ровно два решения
{ (x-3)² + (y+3sqrt(3))²=9
{ (x-4cosφ)^2 + (4-sinφ)^2=1
Решите неравенство: [m]4^x+(x-13)2^x-2x+22<0[/m]
Найдите все положительные а, при каждом из которых любое x из отрезка [ -1/2 ; 1/2] будет являться решением неравенства 3a^(2x)-5*16^x +14(4a)^x ≥ 0

Найдите все значения a, при каждом из которых неравенство |x2– 8x + a + 5| ˃ 10 не имеет решений на отрезке [a – 6; a].
как такое решить? Вижу симметрию, но не понимаю как ее использовать для условия задачи «более двух решений», благодарю за помощь!

Найдите все значения a, при каждом из которых система уравнений
{ sqrt(64 - y²) = sqrt(64 — a²x²),
{ x² + y² = 2x + 8y
имеет ровно два решения.
Найдите все значения a, при каждом из которых система уравнений
{ log5(16 - y^2) = log₅(16 - a^2x^2),
{ x^2 + y^2 = 6x + 4y
имеет ровно два решения.
Найти все значения а,при котором уравнение имеет 4 корня а^2-2*x^2 -a*x- 6*a+3*x+ 9*|x| = 0
при каких значениях параметра а уравнение 64^x+(a-4)*8^x+ 4-2a = 0 имеет один корень
при каких значениях параметра а уравнение х+sqrt(4а-х^2)=sqrt(2ax+4a) имеет единственный корень
при каких a уравнение 2|x| =ax-2 не имеет решений ?
При каком значении параметра решением неравенства ax2 + (2a –1)x + a – 2 ≤ 0 является вся числовая прямая? Укажите его наибольшее значение.
При каком значении параметра уравнение a2x + 4ax – 6a = 12 – 4x имеет бесконечно много корней?
При каких значениях параметра а неравенство 4^x + (а — 1) * 2^x + 2а — 5 >0 выполнено при всех значениях х?

Найти все значения параметра а, при которых уравнение 3*4^x-2 + 27= а + а*4^x-2 имеет хотя бы одно решение.

При каких значениях параметра а уравнение имеет только одно решение?

11(5). Найдите все значения параметра а ‚ при каждом из которых система уравнений (ay+ax—1)(y+x—a)=0, |о]=а имеет ровно четыре решения.
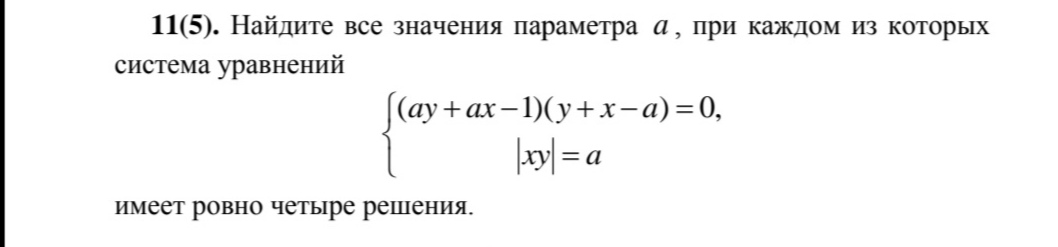
Найдите все а, при которых системаимеет единственное решение: {х1+ Зах + За? + За +3 < 3 т у- 4созу 0 =у < 2
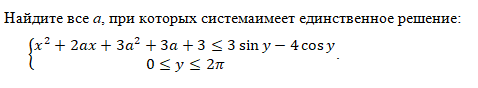
Найдите все значения а, при каждом из которых система уравнений x(x^2+y^2-y-2)=|x|(y-2),y=x+a имеет ровно три различных решения.

Найти все значения параметра a, при каждом из которых система уравнений {(sqrt(16 -y^2)= sqrt(16- a^2 x^2)), (x^2+ y^2= 8x+4y):} имеет ровно два различных решения
x^2-8a+a^2-6x/x^2+a-8=0 Найти все a, при которых. уравнение имеет ровна 2 решение
При каких значениях параметра а множеством неровности sqrt (1- (x + 2a) ^ 2)> = (4/3)x является промежуток длиной 9/5
(9x^2-36x+36)(a-4)/(2^x-a)≥0
Решите неравенство в зависимости от значений параметра.
Параметр.
1)Решите первое неравенство этой системы
2) Определите множество решений второго неравенства системы в зависимости от значений а
3)Определите все решения системы в зависимости от значений а.
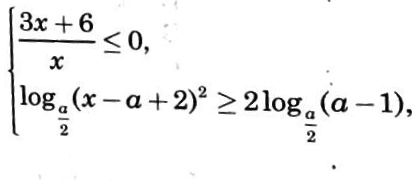
Помогите пожалуйста!! при каком наименьшем [red]a[/red] уравнение имеет хотя бы один корень?
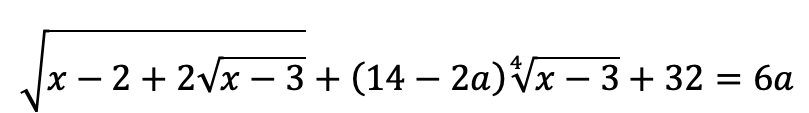
При каких значениях параметра a система
2^(lny)=4^(|x|)
log_(2)(x^(4)y^(2)+2a^(2))=log_(2)(1-ax^(2)y^(2))+1
имеет единственное решение?
(x-2)(x-4)-5(x-2)√((x-4)/(x-2)) =(a-2)(a+3) Найти значения параметра а,при которых равенство имеет только [b]один корень[/b]
sin3x+6cos2x-12sinx=p
При каких значениях параметра р уравнение имеет решение?
18 Найдите все значения параметра a, при каждом из которых уравнение
121^x + (3a^2 - a + 4) * 11^x - 5a - 2 = 0
имеет единственный корень.

(a^3-(x+2)*a^2+xa+x^2)/(a+x)=0
Найдите сумму всех значений а при каждом из которых уравнение имеет ровнотодин корень
64х^(6)+ 4х^(2)= (3х+а)^(3)+3х+а
Найдите все целочисленные значения параметра а, при каждом из которых система
1. sqrt((x-1)^2 + (y-a)^2) + sqrt((x-5)^2 + (y-a)^2) = 4
2. x^2 - |a+1|x - 2a^2 = 3
имеет единственное решение
Найдите все значения а, при каждом из которых уравнение a^2 + 13|x| + 5 sqrt(4x^2+9)= 3a + 3|4x-3a| имеет хотя бы один корень
Найдите все значения а, при каждом из которых уравнение 64x^6 - (3x+a)^3 + 4x^2 - 3x = a имеет более одного корня
Найти все значения параметра а, при каждом из которых уравнение
sin(x+4a) + sin ((x^2 - 6x - 7a)/2) = 4x -x^2 - a
не имеет действительных решений
2. Указать при каком значении параметра т, следующие уравнения имеют бесконечно много решений:
a) 6(тх - 1) - т = 2(т + х) - 7;
б) 0,5(5х - 1) = 4,5 - 2т(х - 1).
3. Указать при каком значении параметра m, следующие уравнения не имеют решения:
а) m²x - m + 1 = 6x - 5mx; б) m²x = m(x + 2) - 2.
При каком значении параметра m уравнение имеет бесконечное множество решений 6(mx-1)-m=2(m+x)-7
При каком значении m уравнение не имеет решения m^2x-m+1=6x-5mx
Все пары положительных чисел (x, y) удовлетворяющих уравнению
log(2x^2y+1)(x^4+y^2+1) = log(y^4+x^2+1)(2xy^2+1)
Срочно нужно.
Найдите все значения параметра a, при каждом из которых уравнение
(9x^(2)-a^(2))/(x^(2)+8x+16-a^(2))=0
имеет ровно два различных корня.
Надо как-то на графике это сделать с прямыми.
Найдите все значения a, при каждом из которых система уравнений
x^(2)+y^(2)-4(a+1)x-2ay+5a^(2)+8a+3=0
y^(2)=x^(2)
имеет ровно четыре различных решения.
Найдите значение параметра а, при которых система уравнений
6x^(2)-5xy+y^(2)+x-y-2=0
y=ax-5
имеет ровно одно решение.
Найдите все значения a, при каждом из которых уравнение
x^(2)+(x-1)*sqrt(2x-a)=x
имеет ровно один корень на отрезке [0;1].

Найдите все значения a, при каждом из которых система
{|x^2 - x - 6| = (y - 1)^2 + x - 7,
{3y = 2x + a
имеет ровно один или два корня
Найдите все значения a, при каждом из которых система уравнений
{ x(x^2 + y^2 - y - 2) = |x|(y - 2),
{ y = x + a
имеет ровно три различных решения.
Найдите все значения a, при каждом из которых система
{y = sqrt(7 + 6x - x^2) + 3,
{y = a + sqrt(16 - a^2 + 2ax - x^2).
имеет единственное решение.
Найдите все значения параметра a, при которых наименьшее значение функции
f(x)=ax−2a−1+|x^2−x−2|
меньше -2
36^x-(8a-1)×6^x+16a^2-4a-2=0
найти все значения параметра а, при каждом из которых уравнение имеет единственный корень
Редакторы (1)


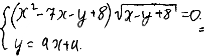

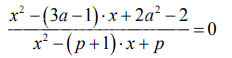
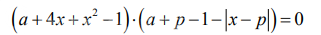






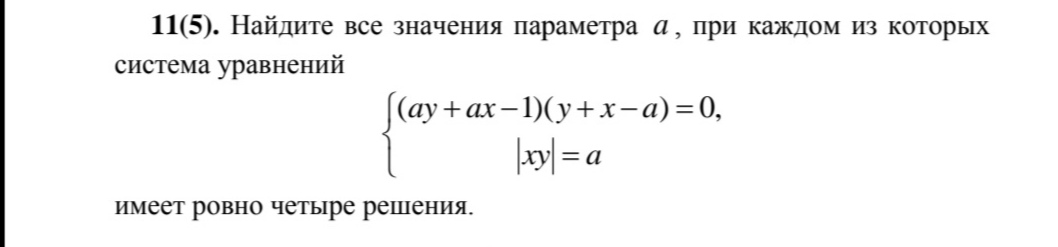
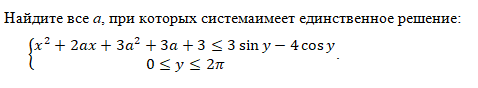


 SOVA
SOVA