Задача 65378 ...
Условие
{ (x-3)² + (y+3sqrt(3))²=9
{ (x-4cosφ)^2 + (4-sinφ)^2=1
Решение
(x-4cos φ )^2+(y-4sin φ )^2=1- уравнение окружности с центром (4cos φ ;4sin φ ) и радиусом 1
При φ =0
получим уравнение
(x-4)^2+y^2=1- уравнение окружности с центром (4;0) и радиусом 1
Данная окружность и полученная не пересекаются.
При φ =30 °
получим уравнение
(x-2sqrt(2))^2+(y-2)^2=1- уравнение окружности с центром (2sqrt(3);2) и радиусом 1
На рисунке окружность сиреневого цвета. Она пересекается с данной окружностью в двух точка
Значит надо определить при каких значениях φ окружность
(x-4cos φ )^2+(y-4sin φ )^2=1 касается данной окружности (x-3)^2+(y-3sqrt(3))^2=9
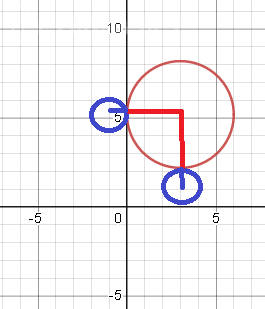
В таком случае расстояние между центрами окружностей равно сумме радиусов 3+1=4.
И тогда условию будут удовлетворять те значения φ, при которых окружности расположены
между крайними положениями касания
[m]\sqrt{(3-4cos φ )^2+(3\sqrt{3}-4sin φ )^2}=4[/m]
Возводим в квадрат
[m](3-4cos φ )^2+(3\sqrt{3}-4sin φ )^2=16[/m]
Решаем ЭТО тригонометрическое уравнение.
Раскрываем скобки:
[m]9-24cos φ +16cos^2 φ +27-24\sqrt{3}sin φ +16sin^2 φ =16[/m]
Так как [m]16cos^2 φ +16sin^2 φ =16(cos^2 φ +sin^2 φ )=16\cdot 1=16[/m]
[m]24cos φ +24\sqrt{3}sin φ =36[/m]
[m]2cos φ +2\sqrt{3}sin φ =3[/m]
Решаем уравнение [i]методом введения вспомогательного угла[/i].
Делим обе части уравнения на 4:
([m] \sqrt{2^2+(2\sqrt{3})^2}=4[/m])
[m]\frac{1}{2}cos φ +\frac{\sqrt{3}}{2}sin φ =\frac{3}{4}[/m]
Вводим вспомогательный угол, например, так:
[m]\frac{1}{2}=cos\frac{π}{3} [/m];[m]\frac{\sqrt{3}}{2}=sin\frac{π}{3} [/m] ⇒
Уравнение принимает вид:
[m]cos\frac{π}{3} cos φ +sin\frac{π}{3} sin φ =\frac{3}{4}[/m] ⇒
[m]cos( φ -\frac{π}{3} )=\frac{3}{4}[/m]
[m]( φ -\frac{π}{3} )= ± arccos \frac{3}{4}+2πn. n ∈ [/m][b]Z[/b]
[m] φ=\frac{π}{3} ± arccos \frac{3}{4}+2πn. n ∈ [/m][b]Z[/b]
О т в е т. [m] \frac{π}{3} - arccos \frac{3}{4}+2πn ≤ φ ≤\frac{π}{3} + arccos \frac{3}{4}+2πn, n ∈ [/m][b]Z[/b]
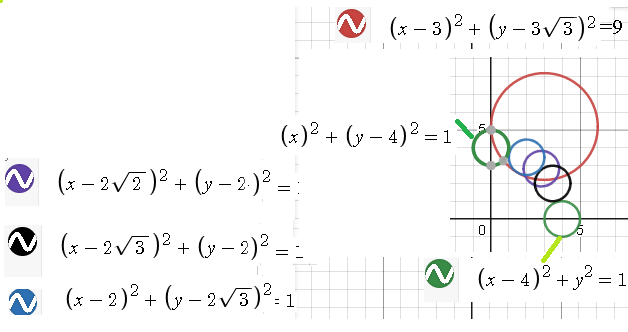
Все решения
(3 - 4cos φ)^2 + (3sqrt(3) - 4sin φ)^2 = 16
9 - 24cos φ + 16cos^2 φ + 27 - 24sqrt(3)sin φ + 16sin^2 φ = 16
Заметим, что:
16cos^2 φ + 16sin^2 φ = 16(cos^2 φ + sin^2 φ) = 16
Поэтому:
36 - 24cos φ - 24sqrt(3)sin φ + 16 = 16
36 - 24cos φ - 24sqrt(3)sin φ = 0
Сокращаем всё на 12 и переносим переменные направо:
3 = 2cos φ + 2sqrt(3)sin φ
Переходим к половинному аргументу:
3cos^2 (φ/2) + 3sin^2 (φ/2) = 2cos^2 (φ/2) - 2sin^2 (φ/2) +
+ 4sqrt(3)sin(φ/2)*cos(φ/2)
Переносим всё налево:
5sin^2 (φ/2) - 4sqrt(3)sin(φ/2)*cos(φ/2) + cos^2 (φ/2) = 0
Делим всё на cos^2 (φ/2):
5tg^2 (φ/2) - 4sqrt(3)*tg (φ/2) + 1 = 0
Получили квадратное уравнение относительно tg (φ/2).
Это уже доступно решить школьнику.