Задача 36466 Найдите все значения параметра a, при...
Условие
f(x)=ax−2a−1+|x^2−x−2|
меньше -2
Все решения
[b]Первый случай[/b]
[b]Если x^2-x-2 ≥ 0[/b]
⇒ |x^2−x−2|=x^2−x−2 при [b]х≤ -1 или x ≥ 2[/b]
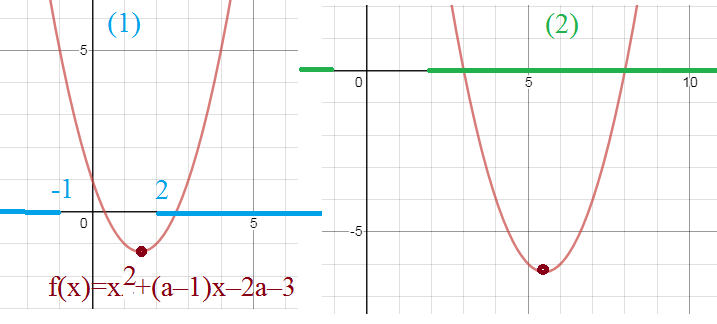
f(x)=x^2+(a-1)x-2a-3
f`(x)=2x+(a-1)
f`(x)=0
2x+(a-1)=0
x=(1-a)/2
y((1-a)/2)=((1-a)/2)^2+(a-1)*(1-a)/2-2a-3=(1-a)^2/4 -(1-a)^2/2 - 2a-3=
=(-(1-a)^2-8a-12)/4=(-a^2-6a-13)/4
Если абсцисса вершины x_(o)=(1-a)/2
находится между точками -1 и 2, т.е
-1 ≤ (1-a)/2 ≤ 2, то наименьшее значение не в вершине [b](!!!)[/b], а в точках x =-1 или x=2 ( cм. рис.1)
f(-1)=(-1)^2+(a-1)*(-1)-2a-3=-3a-1
f(2)=2^2+(a-1)*2-2a-3=-1 >-2
Поэтому
значение параметра а находим из системы
[b](1)[/b]
{-1 < (1-a)/2 < 2⇒ -3 < a < 3
{-3a-1<-2⇒ a > 1/3
О т в е т [b](1)[/b] (1/3;3)
Если абсцисса вершины x_(o)=(1-a)/2 находится вне (-1;2), то наименьшее значение в вершине ( неважно слева от -1
или справа от 2 см. рис. 2)
значение параметра а находим из системы
[b](2)[/b]
{(1-a)/2 ≤ -1 или (1-a)/2 ≥2 ⇒ a≥3 или а ≤ -3
{(-a^2-6a-13)/4<-2 ⇒ a^2+6a+5>0 ⇒ a < -5 или a> -1
О т в е т [b](2)[/b] (-∞; -5) U [3;+∞)
О т в е т первого случая объединение ответов [b](1)[/b] и [b](2)[/b]
(-∞; -5) U (1/3;3)U [3;+∞)= [b](-∞; -5) U (1/3;+∞)[/b]
[b]Второй случай[/b]
[b] Если x^2-x-2 < 0 [/b]
⇒ |x^2−x−2|=-x^2+x+2 при -1 ≤ x ≤ 2
f(x)=-x^2+(a+1)x-2a+1 - графиком служит парабола, ветви которой направлены вниз.
Значит в вершине параболы всегда наибольшее значение.
а наименьшее значение данная функция принимает на концах интервала
либо в точке х=-1 либо в точке х=2
Так как f(2)=-4+2(a+1)-2a+1=-1 > -2
Значит наименьшее значение в точке x=-1
f(-1)=-(-1)^2+(a+1)*(-1)-2a+1=-3a-1
-3a-1 < -2 ⇒ a > 1/3
О т в е т второго случая объединение ответов [b] (1/3;+∞)[/b]
О т в е т. Объединение ответов первого и второго случаев
[b](-∞; -5) U (1/3;+∞)[/b]