Задача 59528 При каких значениях параметра a...

604dc3c4ee495c5c9acb8c84

01.05.2021 18:24:06

При каких значениях параметра a система
2^(lny)=4^(|x|)
log_(2)(x^(4)y^(2)+2a^(2))=log_(2)(1-ax^(2)y^(2))+1
имеет единственное решение?

5f3ea7e3faf909182968ddd9

03.05.2021 10:11:31

★

ОДЗ:
[m]\left\{\begin {matrix}y>0\\x^4y^2+2a^2>0\\1–ax^2y^2>0\end {matrix}\right.[/m]

Так как
2a^2 ≥ 0, то x^4y^2 >0

y>0 ⇒ x ≠ 0



2^(lny)=4^(|x|) ⇒ 2^(lny)=2^(2|x|) ⇒ lny=2|x|

log_(2)(x^4y^2+2a^2)=log_(2)(1–ax^2y^2)+1 ⇒ log_(2)(x^4y^2+2a^2)=log_(2)(1–ax^2y^2)+log_(2)2

⇒
log_(2)(x^4y^2+2a^2)=log_(2)2*(1–ax^2y^2) ⇒

x^4y^2+2a^2=2*(1–ax^2y^2)



[m]\left\{\begin {matrix}y>0\\x ≠ 0\\lny=2|x|\\x^4y^2+2a^2=2\cdot (1–ax^2y^2)\end {matrix}\right.[/m]

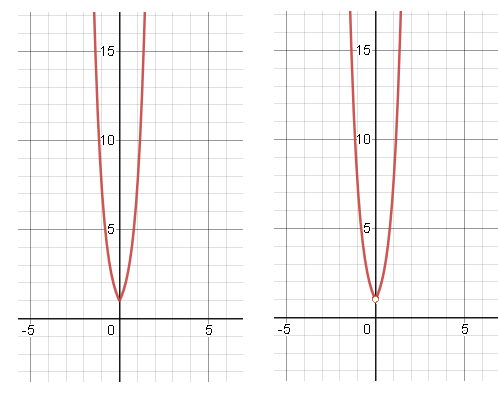
График lny=2|x| на рис. 1
Учесть ОДЗ - значит исключить точку с абсциссой 0

Получим "выколотую" точку (0;1)

Теперь разберемся со вторым уравнением:

x^4y^2+2a^2=2*(1–ax^2y^2) -

y^2*[b](x^2)^2[/b]+2a*y^2*[b]x^2[/b]+2a^2-2=0

Это биквадратное уравнение .

D=(2ay^2)^2-4*y^2*(2a^2-2)=

Здесь мне не очень нравится... Поэтому вопрос по условию... Там все верно? Приложите фото...