Задача 52428 Срочно нужно. Найдите все значения...
Условие
Найдите все значения параметра a, при каждом из которых уравнение
(9x^(2)-a^(2))/(x^(2)+8x+16-a^(2))=0
имеет ровно два различных корня.
Надо как-то на графике это сделать с прямыми.
Решение

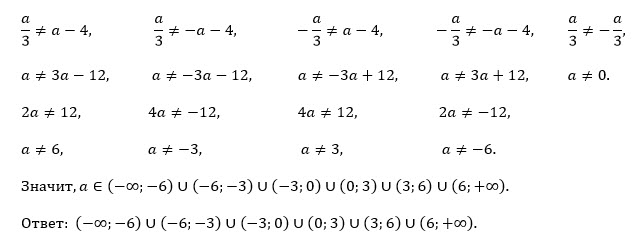

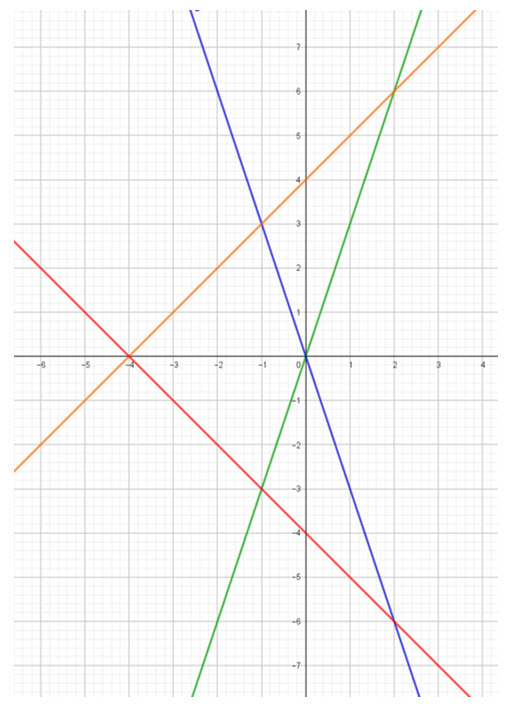

Все решения
{9x^2-a^2=0 ⇒ x=a/3 или x=-a/3
{x^2+8x+16-a^2 ≠ 0
Уравнение имеет два корня x_(1)=a/3; x_(2)=-a/3, если [red]а ≠ 0 [/red] и эти корни не являются корнями знаменателя.
Надо исключить те значения параметра а, при которых корни числителя и знаменателя совпадают.
Для этого можно найти корни x_(3) и x_(4) знаменателя:
x^2+8x+16-a^2 = 0
и решить неравенства:
x_(1) ≠ x_(3);
x_(1) ≠ x_(4)
и
x_(2) ≠ x_(3);
x_(2) ≠ x_(4)
[blue]Можно подставить[/blue] x_(1) и x_(2) во второе неравенство
(a/3)^2+8*(a/3)+16-a^2 ≠ 0 ⇒ a^2-3a-18 ≠ 0 ⇒ a ≠ -3; a ≠ 6
и
(-a/3)^2+8*(-a/3)+16-a^2 ≠ 0 ⇒ a^2+3a-18 ≠ 0 ⇒ a ≠ -3; a ≠ 6
[red]О т в е т. (- ∞ ;-6)U(-6;-3)U(-3;0)ГU(0;3)U(3;6)U(6; + ∞ )[/red]
можно посмотреть решения аналогичных задач:
https://reshimvse.com/zadacha.php?id=47048
https://reshimvse.com/zadacha.php?id=37732
https://reshimvse.com/zadacha.php?id=37757