Задача 52855 ...

slava191

11 июля 2020 г. в 18:59

Найдите все значения a, при каждом из которых система уравнений

{ √64 – y² = √64 — a²x²,
{ x² + y² = 2x + 8y

имеет ровно два решения.

sova

12 июля 2020 г. в 11:52

[m]\left\{\begin{matrix} 64-y^2 ≥ 0\Rightarrow -8 ≤ y ≤ 8\\ 64-a^2x^2 ≥ 0\Rightarrow-8 ≤ ax ≤ 8 \\ 64-y^2=64-a^2x^2\Rightarrow y^2=a^2x^2 \\ (x-1)^2+(y-4)^2=17 \end{matrix}\right.[/m]


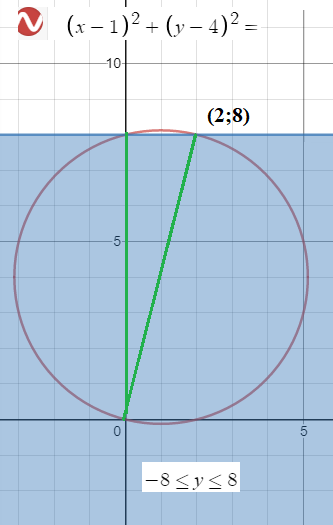
(x–1)²+(y–4)²=17 – уравнение окружности с центром (1;4) и R=√17

причем окружность проходит через начало координат.


y²=a²x² ⇒ |y|=|ax| ⇒ y= ± ax – семейство двух пересекающихся прямых, проходящих через начало координат.

Эти прямые имеют с окружностью три общие точки.(Одна из них (0;0)

Условия 1) и 4)
64–y² ≥ 0
(x–1)²+(y–4)²=17 задают на плоскости область, см. рис.

Поэтому если прямые проходят внутри угла, ограниченного зелеными прямыми, то тогда они имеют только две точки пересечения с окружностью

y=ax

(2;8)

8=a·2

a=4

О т в е т. a > 4