Задача 61060 11(5). Найдите все значения параметра а...
Условие
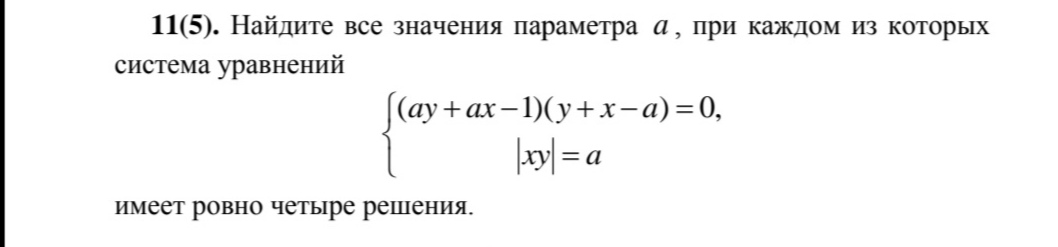
Решение
Система принимает вид:
[m]\left\{\begin {matrix}(ay+ax-1)(y+x-a)=0\\xy=a\\xy ≥0 \end {matrix}\right.[/m]
|xy|==xy, если x и у имеют разные знаки,т.е находятся во 2 и 4 четвертях
Система принимает вид:
[m]\left\{\begin {matrix}(ay+ax-1)(y+x-a)=0\\xy=-a\end {matrix}\right.[/m]
Произведение двух множителей равно 0, если хотя бы один из них равен 0.
Каждая система распадается на две.
Всего 4 системы:
[m]\left\{\begin {matrix}ay+ax-1=0\\xy=a\\xy ≥0 \end {matrix}\right.[/m] или [m]\left\{\begin {matrix}y+x-a=0\\xy=a\\xy ≥0 \end {matrix}\right.[/m]
[m]\left\{\begin {matrix}ay+ax-1=0\\xy=-a\\xy <0\end {matrix}\right.[/m] или [m]\left\{\begin {matrix}y+x-a=0\\xy=-a\\xy<0\end {matrix}\right.[/m]