Задача 52386 Найдите все значения a, при каждом из...

tupiza

12 июня 2020 г. в 19:32

Найдите все значения a, при каждом из которых система уравнений

x²+y²–4(a+1)x–2ay+5a²+8a+3=0
y²=x²

имеет ровно четыре различных решения.

sova

14 июня 2020 г. в 20:47

Решаем способом подстановки

Рассматриваем два случая:
{y=x
{x²+x²–4·(a+1)·x–2a·x+5a²+8a+3=0

или
{y=–x
{x²+x²–4·(a+1)·x–2a·(–x)+5a²+8a+3=0

Решаем второе уравнение первой системы:
2x²–(6a+4)·x+5a²+8a+3=0

D=(6a+4)²–4·2·(5a²+8a+3)=36a²+48a+16–40a²–64a–24=–4a²–16a–8=–4·(a²+4a+2)

Если D >0 уравнение имеет два корня, система два решения:
a²+4a+2 < 0⇒ [m]-2-\sqrt{2} < x < -2+\sqrt{2}[/m]


Решаем второе уравнение первой системы:
2x²–(2a+4)·x+5a²+8a+3=0

D=(2a+4)²–4·2·(5a²+8a+3)=4a²+16a+16–40a²–64a–24=–36a²–48a–8=–4·(9a²+12a+2)

D>0, уравнение имеет два корня, система два решения:

9a²+12a+2<0 ⇒ [m]\frac{-2-\sqrt{2}}{3} < x < \frac{-2+\sqrt{2}}{3}[/m]

⇒ первая и вторая система имеют 4 решения при a ∈ ( [m]\frac{-2-\sqrt{2}}{3}; -2+\sqrt{2}[/m]):

(–2–√2) ____ ([m]\frac{-2-\sqrt{2}}{3}[/m]) \\\\\\\\\ (–2+√2) ____ ([m]\frac{-2+\sqrt{2}}{3}[/m])

2 способ Графический:

Выделяем полные квадраты в первом уравнении:

(x²–4(a+1)x+(2a+2)²)+(y²–2ay+a²)–(2а+2)²–a²+5a²+8a+3=0

(x–(2a+2))²+(y–a)²=1

– уравнение окружности с центром в точке (2а+2;а) R=1

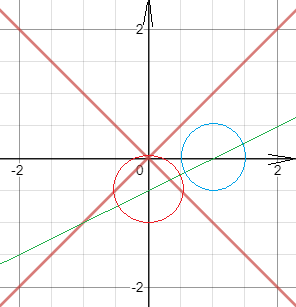
y²=x² ⇒ |y|=|x| ⇒ y= ± |x| – две вертикальные прямые – биссектрисы 1–3 и 2–4 углов

Переформулируем задачу: при каких значения параметра а окружность пересекает прямые y= ± |x| в четырех точках

( см. рис.)

x_o=2a+2
y_o=a ⇒

центры окружностей находятся на прямой x=2y+2


Окружность x²+(y–1)²=1 имеет с прямыми три общие точки.

Сдвиг влево, про прямой x=2y+2 приведет к тому, что точек пересечения менее четырех.

Значит двигаем вправо.

(x–2)²+y²=1 не имеет точек пересечения с прямыми.

Значит окружности расположены между красной и синей.

Как найти значения а при этом затрудняюсь ответить. См аналитическое решение выше.