Задача 59756 Параметр. 1)Решите первое неравенство...
Условие
1)Решите первое неравенство этой системы
2) Определите множество решений второго неравенства системы в зависимости от значений а
3)Определите все решения системы в зависимости от значений а.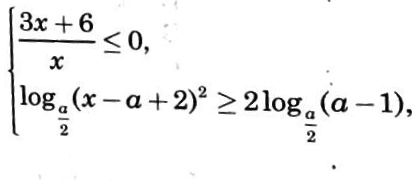
Решение
[m]\frac{3x+6}{x} ≤ 0[/m]
Решаем методом интервалов:
[i]нуль числителя[/i]
3х+6=0
х=-2
[i]нуль знаменателя[/i]
__+____ [-2] ____-___ (0) ______+_____
-2 ≤ x <0
2) Определите множество решений второго неравенства системы в зависимости от значений а
[m]log_{\frac{a}{2}} (x-a+2)^2 ≥ 2log_{\frac{a}{2}} (a-1)[/m]
ОДЗ:
[m]\left\{\begin {matrix}\frac{a}{2}>0\\\frac{a}{2} ≠1\\ (x-a+2)^2>0\\a-1 >0 \end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}a>0\\a ≠2\\ x-a+2 ≠ 0\\a >1 \end {matrix}\right.[/m] ⇒
[m]\left\{\begin {matrix} x ≠ a-2\\a >1, a ≠2 \end {matrix}\right.[/m]
[m]log_{\frac{a}{2}} (x-a+2)^2 ≥ log_{\frac{a}{2}} (a-1)^2[/m]
если [m] 1< a < 2[/m] , то основание логарифмической функции [m] 0 <\frac{a}{2}<1[/m],
логарифмическая функция убывает: [i]бОльшему[/i]у значению функции соответствует [i]мЕньшее[/i] значение аргумента
Получаем систему:
[m]\left\{\begin {matrix} 1< a < 2 \\(x-a+2)^2 ≤ (a-1)^2 \end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix} 1< a < 2 \\(x-a+2)^2 - (a-1)^2 ≤ 0\end {matrix}\right.[/m]⇒
[m]\left\{\begin {matrix} 1< a < 2 \\((x-a+2) - (a-1))\cdot((x-a+2) + (a-1)) ≤ 0\end {matrix}\right.[/m]⇒
[m]\left\{\begin {matrix} 1< a < 2 \\(x-2a+3)\cdot((x+1) ≤ 0\end {matrix}\right.[/m]
если [m] a > 2[/m] , то основание логарифмической функции [m] \frac{a}{2}>1[/m],
логарифмическая функция функция возрастает:[i]бОльшему[/i]у значению функции соответствует [i]бОльшее[/i] значение аргумента
Получаем систему:
[m]\left\{\begin {matrix} a > 2 \\(x-a+2)^2 ≥ (a-1)^2 \end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix} a > 2 \\(x-a+2)^2-(a-1)^2 ≥ 0 \end {matrix}\right.[/m] ⇒
[m]\left\{\begin {matrix} a > 2 \\((x-a+2) - (a-1))\cdot((x-a+2) + (a-1)) ≥ 0 \end {matrix}\right.[/m] ⇒
[m]\left\{\begin {matrix} a > 2 \\(x-2a+3)\cdot((x+1) ≥ 0 \end {matrix}\right.[/m]