Задача 59364 ...
Условие
Решение
ОДЗ:
[m]\frac{x–4}{x–2} ≥0[/m] ⇒
x<2 или x ≥ 4
В условиях ОДЗ можно переписать уравнение в виде:
[m](x–2)(x–4)–5\sqrt{(x–2)\cdot (x–4)} =(a–2)(a+3)[/m]
Замена переменной:
[m]\sqrt{(x–2)\cdot (x–4)}=t[/m]
тогда
[m](x–2)(x–4)=t^2[/m]
Решаем квадратное уравнение:
[m]t^2–5t -(a–2)(a+3)=0[/m]
D=25+4(a-2)(a+3)=4a^2+4a+1=(2a+1)^2
t_(1)=a+3 или t_(2)=2-a
Обратный переход
[m]\sqrt{(x–2)\cdot (x–4)}=a+3[/m] или [m]\sqrt{(x–2)\cdot (x–4)}=2-a[/m]
По требованию задачи данное уравнение должно иметь только[b] один корень[/b].
Это означает, что либо первое уравнение имеет один корень, либо второе уравнение имеет один корень
Поэтому переформулируем требование задачи.
При каких значениях параметра а только одно уравнение
[m]\sqrt{(x–2)\cdot (x–4)}=a+3[/m] или [m]\sqrt{(x–2)\cdot (x–4)}=2-a[/m]
имеет один корень, удовлетворяющий ОДЗ.
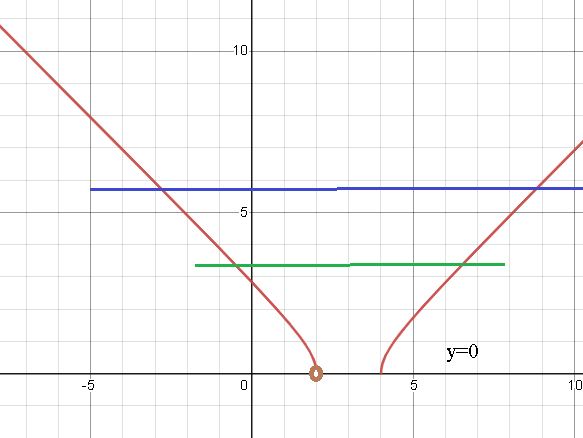
Решаем графически ( cм. рис.)
График левой части уравнения с учетом ОДЗ см. на рис.
Любая прямая y=b, b >0 имеет с кривой две точки пересечения.
Любая прямая y=с, с <0 не имеет с кривой точек пересечения.
Прямая y=0 имеет с кривой ОДНУ общую точку.
Поэтому при a+3=0 , т.е при a=-3 уравнение: [m]\sqrt{(x–2)\cdot (x–4)}=a+3[/m] имеет один корень
х=4
НО второе уравнение [m]\sqrt{(x–2)\cdot (x–4)}=2-a[/m] при этом значении параметра
принимает вид:
[m]\sqrt{(x–2)\cdot (x–4)}=5[/m] и имеет еще два корня.
При 2-a=0, т. е при a=2 второе уравнение [m]\sqrt{(x–2)\cdot (x–4)}=2-a[/m] имеет один корень x=4
НО первое уравнение [m]\sqrt{(x–2)\cdot (x–4)}=a+3[/m] при этом значении параметра
принимает вид:
[m]\sqrt{(x–2)\cdot (x–4)}=5[/m] и имеет еще два корня.
О т в е т. Нет таких значений.