Задача 63194 при каких значениях параметра а...

6209ed38eb82603b2a8ab478

14.02.2022 08:57:14

при каких значениях параметра а уравнение х+sqrt(4а-х^2)=sqrt(2ax+4a) имеет единственный корень

5f3ea7e3faf909182968ddd9

14.02.2022 17:56:03

★

Иррациональное уравнение с параметром.

Находим ОДЗ:

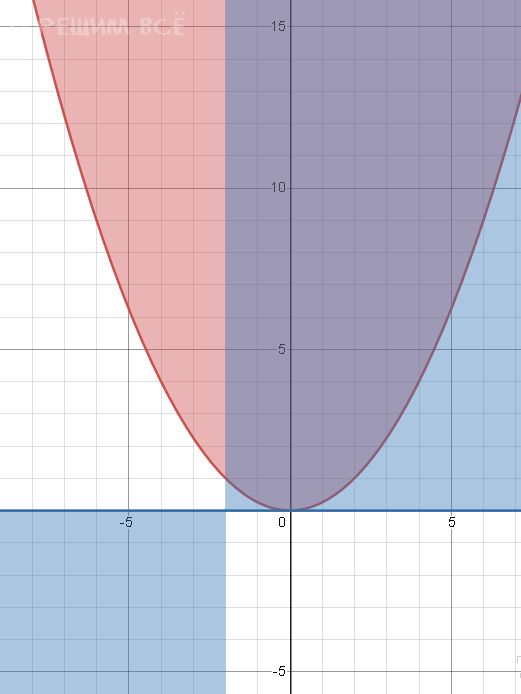
[m]\left\{\begin {matrix}4a-x^2 ≥ 0\\2ax+4a ≥ 0\end {matrix}\right.[/m]

Изображаем решение неравенств на координатной плоскости xOa


Теперь решаем.

Возводим в квадрат:

[m]x^2+2x\sqrt{4a-x^2}+4a-x^2=2ax+4a[/m]

[m]2x\sqrt{4a-x^2}=2ax[/m]

[m]2x\sqrt{4a-x^2}-2ax=0[/m]

[m]2x(\sqrt{4a-x^2}-a)=0[/m]

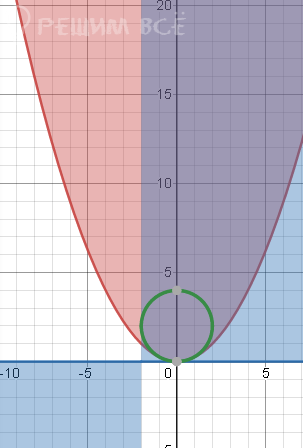
[m]x=0[/m] или [m]\sqrt{4a-x^2}-a=0[/m] ⇒ [m]4a-x^2=a^2[/m] ⇒[m] x^2=(4a-a^2) [/m]⇒[m] x^2+a^2-4a=0[/m]⇒[m] x^2+(a-2)=4[/m] - уравнение окружности на координатной плоскости xOa

Теперь с учетом ОДЗ и вопроса задачи выбираем ответ