Задача 59480 Помогите пожалуйста!! при каком...
Условие
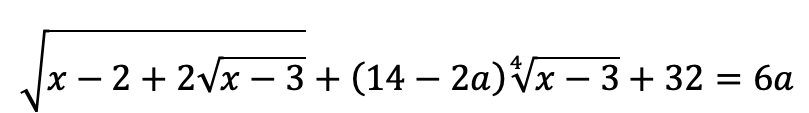
математика 10-11 класс
529
Решение
★
Замена переменной:
[m]\sqrt[4]{x-3}=t[/m] ⇒ [m]\sqrt[2]{x-3}=t^2[/m] ⇒ [m]x-3=t^4[/m] ⇒ [m]x-2=t^4+1[/m] ⇒
Тогда уравнение принимает вид:
[m]\sqrt{t^4+1+2t^2}+(14-2a)t+32=6a[/m]
[m]\sqrt{(t^2+1)^2}+(14-2a)t+32=6a[/m]
[m]|t^2+1|+(14-2a)t+32=6a[/m]
[m]t^2+1+(14-2a)t+32=6a[/m]
Квадратное уравнение с параметром.
[m]t^2+(14-2a)t+(33-6a)=0[/m]
D=(14-2a)^2-4*(33-6a)=...
Если D ≥ 0 уравнение имеет хотя бы один корень, причем этот корень должен удовлетворять ОДЗ:
x-3 ≥ 0
[b]x ≥ 3[/b]