Задача 64212 ...

62619dfec7c98d1fdd9c1e87

21.04.2022 21:12:31

Найдите все положительные а, при каждом из которых любое x из отрезка [ -1/2 ; 1/2] будет являться решением неравенства 3a^(2x)-5*16^x +14(4a)^x ≥ 0

5f3ea7e3faf909182968ddd9

21.04.2022 21:30:47

★

Это однородное неравенство вида [m]a\cdot u^2+b\cdot u\cdot v+c\cdot v^2 ≥ 0[/m]

Решают делением на u^2 ≠ 0 или v^2 ≠ 0

Разделим на[m] 4^{2x}[/m]

Получим неравенство:

[m]3\cdot (\frac{a}{4})^{2x}+14\cdot (\frac{a}{4})^{x}-5 ≥ 0[/m]

Замена переменной

[m](\frac{a}{4})^{x}=t[/m]

D=196+60=256

[m]t_{1}=\frac{-14-16}{6}[/m] или [m]t_{2}=\frac{-14+16}{6}[/m]

[m]t_{1}=\frac{-15}{3}[/m] или [m]t_{2}=\frac{1}{3}[/m]

[m] (\frac{a}{4})^{x}≤ \frac{-15}{3}[/m] или [m](\frac{a}{4})^{x} ≥ \frac{1}{3}[/m]

первое неравенство не имеет решений


[m](\frac{a}{4})^{x} ≥ \frac{1}{3}[/m]

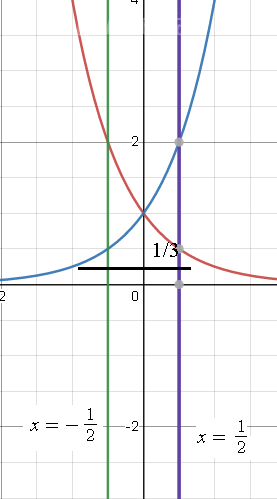
x ∈ [ –1/2 ; 1/2]

[b]Исследуем.[/b]


Рассматриваем два случая

1)
[m]\frac{a}{4}>1[/m]

Показательная функция возрастает

x ∈ [ –1/2 ; 1/2] ⇒ (\frac{a}{4})^{-\frac{1}{2}} ≤ y ≤ (\frac{a}{4})^{\frac{1}{2}}

[m]\left\{\begin {matrix}\frac{a}{4}>1\\(\frac{a}{4})^{-\frac{1}{2}} ≤ \frac{a}{4})^{x} ≤ (\frac{a}{4})^{\frac{1}{2}}\\(\frac{a}{4})^{x} ≥ \frac{1}{3}\end {matrix}\right.[/m]

2)

[m]0<\frac{a}{4}<1[/m]

Показательная функция убывает

[m]\left\{\begin {matrix}0<\frac{a}{4}<1\\(\frac{a}{4})^{\frac{1}{2}} ≤\frac{a}{4})^{x} ≤ (\frac{a}{4})^{-\frac{1}{2}}\\(\frac{a}{4})^{x} ≥ \frac{1}{3}\end {matrix}\right.[/m]