Задача 64081 Решите неравенство:...

604dc3c4ee495c5c9acb8c84

16.04.2022 13:12:32

Решите неравенство: [m]4^x+(x-13)2^x-2x+22<0[/m]

5f3ea7e3faf909182968ddd9

16.04.2022 22:36:41

★

Замена переменной:
[m]2^{x}=t[/m]

[m]t^2+(x-13)\cdot t+22-2x <0[/m]

D=(x-13)^2-4\cdot (22-2x)=x^2-26x+169-88+8x=x^2-18x+81=(x-9)^2

t_(1)=(-(x-13)-(x-9))/2; t_(2)=(-(x-13)+(x-9))/2

t_(1)=(-(x-13)-(x-9))/2; t_(2)=(-(x-13)+(x-9))/2

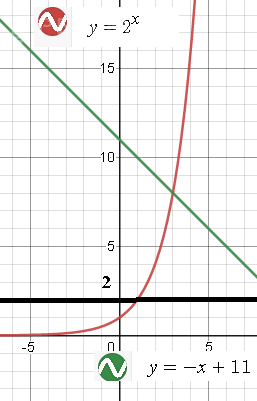
t_(1)=-x+11; t_(2)=2

Рассматриваем два случая:

1) t_(1) < t_(2)

тогда

[m]-x + 11 < 2^{x} < 2[/m]

2)t_(1) > t_(2)

тогда

[m]2 < 2^{x} < -x+11[/m]

Получаем совокупность систем:

[m]\left\{\begin {matrix}-x+11<2\\-x + 11 < 2^{x} < 2\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}-x+11>2\\2 < 2^{x} < -x+11\end {matrix}\right.[/m]

Первая система не имеет решений

Вторая система имеет решение (1;3)