Задача 54946 Найдите все целочисленные значения...

5f6852d13934fb23001a34cf

25.10.2020 01:06:14

Найдите все целочисленные значения параметра а, при каждом из которых система
1. sqrt((x-1)^2 + (y-a)^2) + sqrt((x-5)^2 + (y-a)^2) = 4
2. x^2 - |a+1|x - 2a^2 = 3
имеет единственное решение

5f3ea7e3faf909182968ddd9

25.10.2020 08:49:50

★

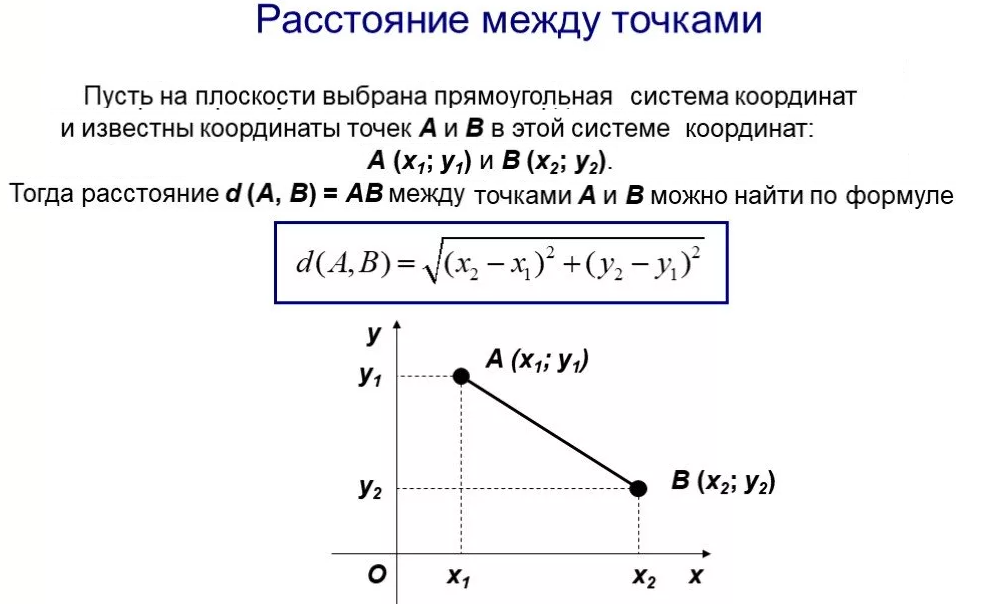
[m]\sqrt{(x–1)^2 + (y–a)^2}[/m] ( см. приложение) -

геометрически означает расстояние между двумя точками M(x;y) и А(1;a)

[m]\sqrt{(x–5)^2 + (y–a)^2}[/m] -
геометрически означает расстояние между двумя точками M(x;y) и B(5;a)

причем точки А и В лежат на одной прямой [m] y=a [/m] и расстояние

[m] AB=5-1=4[/m]


Первое уравнение:

[m]\sqrt{(x–1)^2 + (y–a)^2}+\sqrt{(x–5)^2 + (y–a)^2}=4[/m] геометрически означает, что сумма расстояний

между двумя точками M(x;y) и А(1;a) и между двумя точками M(x;y) и B(5;a) равна АВ

А это означает, что точка М лежит на прямой [m] y=a [/m]

[m]1 ≤ x ≤ 5[/m]

Остается решить второе уравнение с параметром, при условии [m]1 ≤ x ≤ 5[/m]