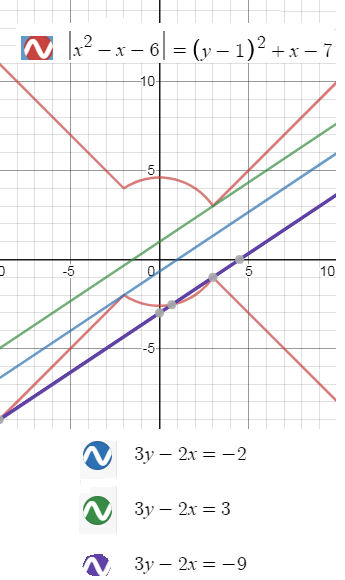
Задача 52162 Найдите все значения a, при каждом из...

vk1060734

5 июня 2020 г. в 16:51

Найдите все значения a, при каждом из которых система

{|x² – x – 6| = (y – 1)² + x – 7,
{3y = 2x + a

имеет ровно один или два корня

sova

5 июня 2020 г. в 21:55

★

Решаем способом подстановки:
{$y=\frac{2x+a}{3}$
{|x²–x–6|=($\frac{2x+a}{3}$–1)²+x–7;

Решаем второе уравнение:

|x²–x–6|=($\frac{2x+a}{3}$)²–2·($\frac{2x+a}{3}$)+1+x–7;

|x²–x–6|=$\frac{4x^2+(4a-3)x+a^2-6a-54}{9}$

Рассматриваем два случая

1)
x²–x–6 ≥0 ⇒ |x²–x–6|=x²–x–6

x²–x–6=$\frac{4x^2+(4a-3)x+a^2-6a-54}{9}$

5x²–(4a+6)·x–a²+6a=0

D=(4a+6)²–20(–a²+6a)=36(a–1)² ≥ 0

x_1,2=$\frac{4a+6 ± 6(a-1)}{10}$

при a=1;

x=1 не удовл условию x²–x–6 ≥ 0

при a ≠ 1
x₁=$\frac{4a+6 -6(a-1)}{10}$;x₂=$\frac{4a+6 +6(a-1)}{10}$;

x₁=$\frac{6 -a)}{5}$;x₂=$a$;

Корни должны удовлетворять условию x²–x–6 ≥ 0


{{a²–a–6 ≥ 0 ⇒ a ≤ –2 или a ≥ 3
{$(\frac{6 -a)}{5})^2-\frac{(6 -a)}{5}$–6 ≥ 0 ⇒ a²–7a–144 ≥ 0 ⇒ a ≤ –9;a ≥ 16
О т в е т случай 1)
a ≤ –9 или a ≥ 16


2)
x²–x–6 < 0 ⇒ |x²–x–6|=–x²+x+6

–x²+x+6=$\frac{4x^2+(4a-3)x+a^2-6a-54}{9}$

13x²+(4a–12)x+a²–6a–108=0

D=(4a–12)²–52(a²–6a–108)=–36a²+216a+5760=–36·(a²–6a–160)

D ≥ 0 ⇒ a²–6a–160 ≤ 0 ⇒ a₁=–5; a₂=16 ⇒ –5 ≤ a ≤ 16

При этом корни:
x₃=$\frac{-4a+12 -6\sqrt{-a^2+6a+160}}{26}$;x₂=$\frac{-4a+12 +6\sqrt{-a^2+6a+160}}{26}$;

должны удовлетворять условию x²–x–6 < 0


Cм графическое решение:

О т в е т. (– ∞ ;–9)U(–9;–2] U[3;+ ∞ )