Дифференциальные уравнения второго порядка и более с постоянными коэффициентами
Практика (53)
y''tg(x) = y' + 1
y''+9y=2sinxsin2x ; y(0)=y(π/2)=0
y'' - 2y' + y = e^x / (x^2+1), y(0) = 0, y'(0) = 0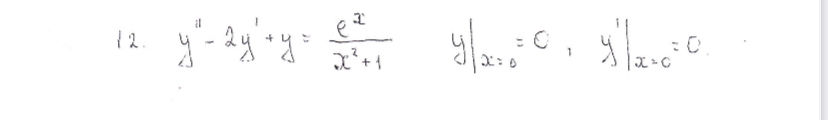
y'' - 9y' = 3x^2+3x+1
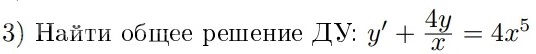
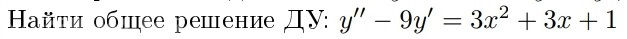
y"-y'=4e^x
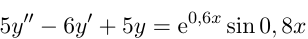

если y=1, y'=-4 при x=0
2)
если S=-8, S'=3 при t=-1
3)y''-4y'+13y=0
если y=-3, y'=9 при x=0
y''-8y'+7y=x^2
xy'=y*ln(y)
Если возможно произвести замену для понижения порядка дифференциального уравнения, то нужно воспользоваться этим, а потом в ходе решения обязательно вернуться к исходной переменной.
Помните: в результате интегрирования дифференциального уравнения должно получиться семейство функций, зависящих от двух произвольных постоянных С1 и С2 .

1)y''+6y'=0;
Помогите решить пожалуйста

y''+y=tg^2(x)
удовлетворяющее начальным условиям.
y'cos^2(x)+y=tg(x), y(0)=-1 
1) xy'–y=√x^2+y^2
2) (1–x^2)y'–2xy=1+x^2
3. Решить ДУ второго порядка и выполнить проверку
1) y''–4y'+4y=0
Помогите пожалуйста
y(0)=0 y'(0)=0
1) y’’+1,44y=0, y(0)=1, y’(0)=0
2)y’’=sin(x/2), y(pi)=pi, y’(pi)=1
y" - 2y' + y = 2e^x/(x^2 +6x+8)
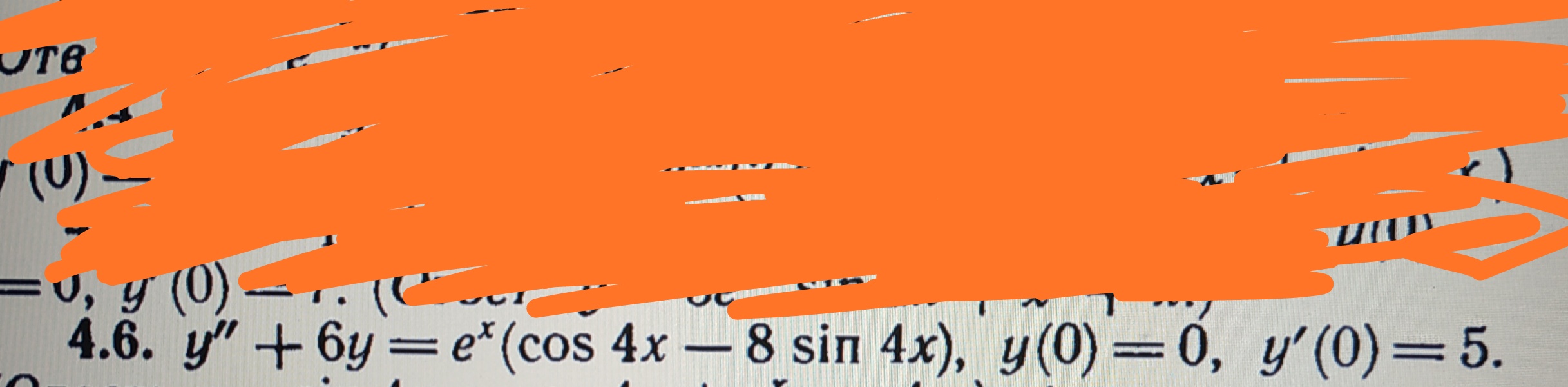
у”-2у’+у=0, у(0)=1, у’(0)=3
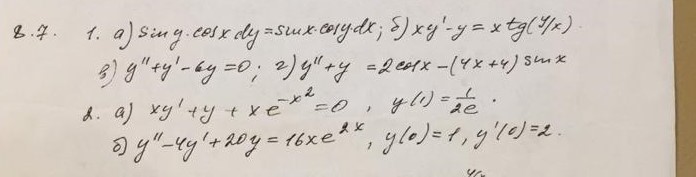
для t > 0 y"(t)+4y(t) = 8e^(2t) , y(0)= 0, y'(0)=3.
удовлетворяющее начальным условиям.

y"-8y'+16y=0
Найти частное решение
y"+ y`- 6y=0
если y=3 , y'= 1 при x=0
y"-5y'+6y=0 ;
y"+y'-6y=0
Найдите общее решение
y"–8y'+16y=0
{ y'' - 10y' + 16y = 0;
{ y = 4; y' = 26, при x = 0.
y"'+y"=10sinx+6cosx+4e^x
y''−4y'+13y=0, y(0)=α, y'(0)=0;
Навигация
- Уравнения с разделяющимися переменными
- Линейные уравнения первого порядка
- Однородные уравнения первого порядка
- Уравнения в полных дифференциалах
- Дифференциальные уравнения второго порядка и более с постоянными коэффициентами
- Системы диф ур
- Уравнения, допускающие понижение порядка
- Решение в виде ряда