Задача 51998 Задание на картинке...
Условие
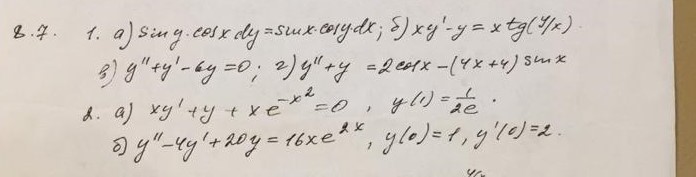
Решение
a)sinycosx dy =sinxcosy dx - уравнение[i] с разделяющимися переменными[/i]
[m]\frac{siny}{cosy}dy=\frac{sinx}{cosx}dx[/m]
Интегрируем:
[m] ∫ \frac{siny}{cosy}dy= ∫ \frac{sinx}{cosx}dx[/m]
[m] - ∫ \frac{d(cosy)}{cosy}=- ∫ \frac{d(cosx)}{cosx}[/m]
[m] ∫ \frac{d(cosy)}{cosy}= ∫ \frac{d(cosx)}{cosx}[/m]
формула ∫ du/u=ln|u|
ln|cosy|=ln|cosx)+lnC ⇒
[b]cosy=C*cosx[/b]- общее решение
-------------
б) Делим обе части уравнения на х:
y`-(y/x)=tg(y/x) [red](#)[/red]
Это [i]однородное уравнение первой степени[/i].
[b]Замена :[/b]
y/x=u
y=x*u
y`=x`*u+x*u` ( x`=1, так как x - независимая переменная)
y`=u+x*u`
Подставляем в [red](#)[/red]
u+x*u`-u=tgu
x*u`=tgu - уравнение с разделяющимися переменными:
u`=du/dx
x*(du/dx)=tgu ⇒ du/tgu=dx/x ⇒ ∫ du/tgu= ∫ dx/x ⇒ ln|u|=ln|x|+lnC ⇒
u=Cx- общее решение.
-----------------
в)
[i]Составляем характеристическое уравнение[/i]
k^2+k-6=0
D=1+24=25
k_(1)=-3; k_(2)=2
два действительных различных корня
Общее решение однородного уравнения пишем по правилу
( см таблицу в приложении 1)
у=C_(1)e^(-3x)+C_(2)e^(2x)
----------------------------------
г)
Это линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Решаем линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами:
y''+y=0
[i]Составляем характеристическое уравнение:[/i]
k^2+1=0
k_(1)=–i; k_(2)=i – корни комплексные
поэтому общее решение однородного уравнения с постоянными коэффициентами имеет вид ( cм таблицу приложение 1, третья строка)
[b]y_(общее одн)=C_(1)cosx+C_(2)sinx – общее решение однородного уравнения[/b]
Правая часть неоднородного уравнения f(x)=2cosx-(4x+4)sinx
имеет так называемый ''специальный'' вид, поэтому частное решение
находим в виде
y_(част)(x)=((Aх+В)cosx+(Mx+N)sinx)*x
( cм. таблицу приложения 2, пункт 5 :
0+i=k_(2)– корень характеристического уравнения кратности 1, поэтому умножаем на x^((1)) )
y_(част)(x)=(Aх^2+Вx)cosx+(Mx^2+Nx)sinx
Находим
y`_(част)=(Aх^2+Вx)`*cosx+(Aх^2+Вx)(cosx)`+(Mx^2+Nx)`*sinx+(Mx^2+Nx)*(sinx)`
y`_(част)=(2Ax+B+Mx^2+Nx)*cosx+(2Mx+N-Ax^2-Bx)*sinx
y``_(част)=(2A+2Mx+N)*cosx-(2Ax+B+Mx^2+Nx)*sinx+
+(2M-2Ax-B)*sinx+(2Mx+N-Ax^2-Bx)*cosx
y``_(част)=(2A+4Mx+2N-Ax^2-Bx)*cosx+(2M-4Ax-2B-Mx^2-Nx)*sinx
подставляем в данное уравнение, находим А, В, M, N
(2A+4Mx+2N-Ax^2-Bx)*cosx+(2M-4Ax-2B-Mx^2-Nx)*sinx+(Aх^2+Вx)cosx+(Mx^2+Nx)sinx=2cosx-(4x+4)sinx
(2A+4Mx+2N)*cosx+(2M-4Ax-2B)*sinx=2cosx-(4x+4)sinx
2А+4Mx+2N=2 ⇒ M=0 и 2А+2N=2
2M-4Ax-2B=-4x-4 ⇒ -4A=-4 ⇒ A=1 и 2M-2B=-4
M=0
A=1
N=0
B=2
y_(част)(x)=х^2cosx
y_(общее неодн)=у_(общее одн)+у_(част)=
=C_(1)cosx+C_(2)sinx+х^2cosx



