Уравнения с разделяющимися переменными
Практика (30)
2. Найти частные решения дифференциальных уравнений, удовлетворяющих начальным условиям: 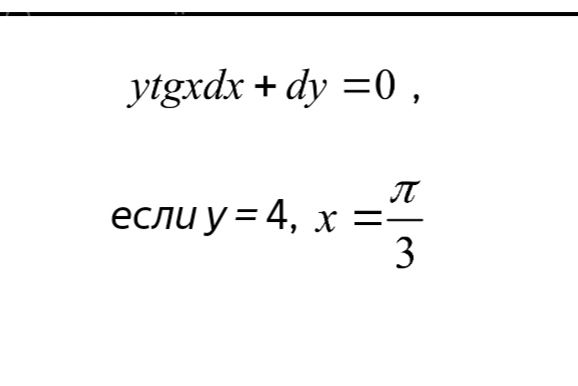
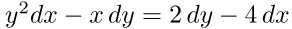

1)найти общее решение ДУ 1-го порядка с разделяющимися переменными: xyy’=1+y^2
2)найти общее решение однородного ДУ 1-го порядка: xy’=y+xe^(x/2)
Выделить полный квадрат.
После этого перейти к разделению переменных.
Помните: в результате интегрирования дифференциального уравнения должно получиться семейство функций. 
а) y' = 7^(x+y)
б) e^(-y) (1 + y') = 1
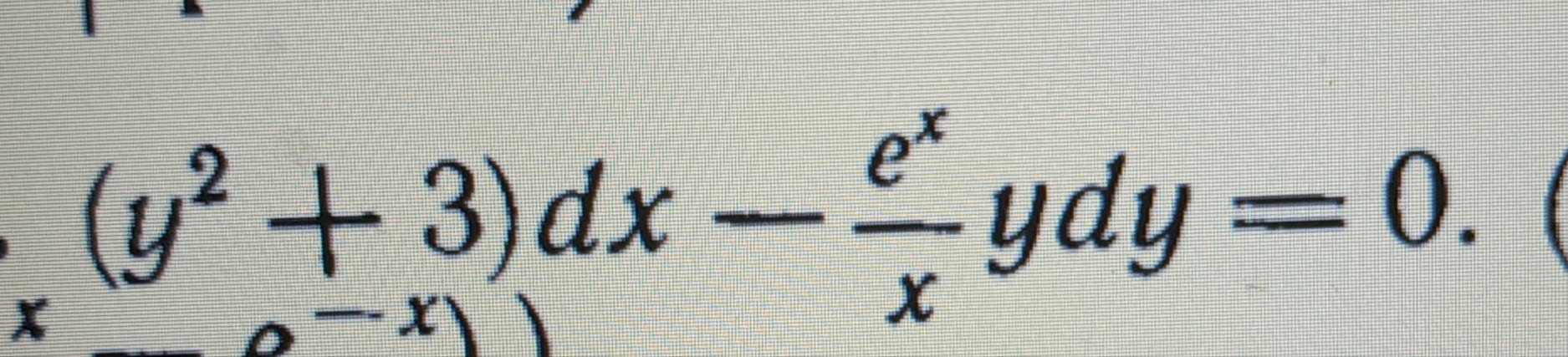
dy/dx = y ∙ cosx; у = 1 при х= 0
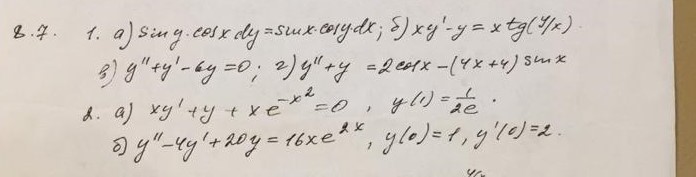
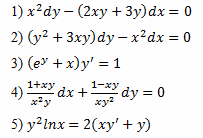
(x+xy^2)dx+(1+x^2)dy=0
а) (1 + e^x)y y' = e^x
б) (1 + y^2)dx = (y - sqrt(1 + y^2))(1 + x^2)dy
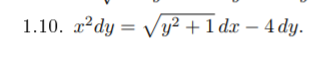
Подставить в общее решение дифференциального уравнения первого порядка заданные начальные условия, выразив затем константу.
Получить частное решение дифференциального уравнения первого порядка. 
(1-2x)y'=1, y(0)=1
3y^2 dy = x^2 dx, y(3) = 1
Найти общее решение дифференциального уравнения ctg x cos^2 y dx + sin^2 x tg y dy = 0
(1+e^x)ydy - αe^xdx = 0
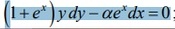
Навигация
- Уравнения с разделяющимися переменными
- Линейные уравнения первого порядка
- Однородные уравнения первого порядка
- Уравнения в полных дифференциалах
- Дифференциальные уравнения второго порядка и более с постоянными коэффициентами
- Системы диф ур
- Уравнения, допускающие понижение порядка
- Решение в виде ряда