Уравнения, допускающие понижение порядка

Решить уравнение y'' + (y')^2 = 2e^(-y)

Решить дифференциальное уравнение, допускающее
понижение порядка

a) y'' = e^(2x),
b) y''y^3 + 25 = 0, y(2)=-5, y'(2)=-1.

Дифференциральное уравнение
y'''sin^4(x)=sin(2x)

Найти частное решение дифференциального уравнения и вычислить значение полученной функции y=ф(x) при x=x0 с точностью до 2 знаков после запятой

Определить тип дифференциального уравнения.
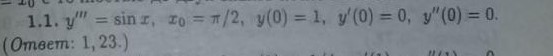
Если возможно произвести замену для понижения порядка дифференциального уравнения, то нужно воспользоваться этим, а потом в ходе решения обязательно вернуться к исходной переменной.
Помните: в результате интегрирования дифференциального уравнения должно получиться семейство функций, зависящих от двух произвольных постоянных С1 и С2 .

Помогите решить 6 дифферинциалов

Задание 1. Найдите общее решение
а) y' = 7^(x+y)
б) e^(-y) (1 + y') = 1

Найти частное решение дифференциального уравнения и вычислить значение полученной функции y=ф(x) при x=x0 с точностью до 2 знаков после запятой

Решить ДУ. Решить задачу Коши для ДУ второго порядка :
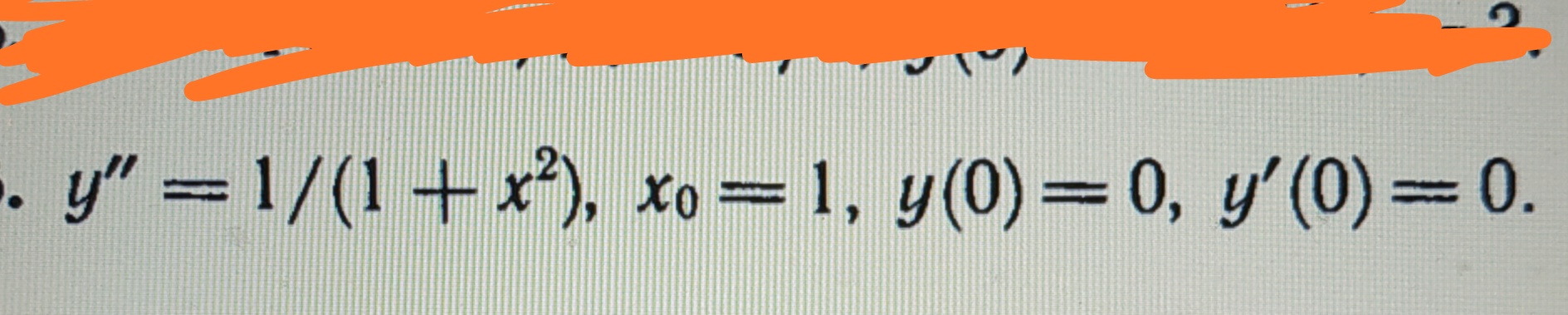
1) y’’+1,44y=0, y(0)=1, y’(0)=0
2)y’’=sin(x/2), y(pi)=pi, y’(pi)=1

y’’+y’tgx=cosx. y(0)=1. y’(0)=0

x(y'' + 1) + y' = 0

2. Решите задачу Коши.
А) y' - 3x² - 6x + 7 = 0, y(1) = 6

2. Решить задачу Коши:
[m]
\begin{cases}
y'' = \sin x; \\
y(\frac{\pi}{2}) = \pi, \; y'(\frac{\pi}{2}) = 2.
\end{cases}
[/m]

найти общее решение дифференциального уравнения