Задача 55203 Найти частное решение дифференциального...
Условие
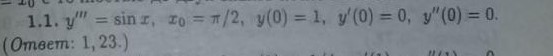
1178
Решение
★
y`(x)= ∫y``(x)dx =∫( -cosx+C_(1))dx=-sinx+C_(1)x+C_(2)
y(x)= ∫y`(x)dx=cosx+C_(1)*(x^2/2)+C_(2)x+C_(3)
---
y(0)=1 ⇒1= cos0+C_(1)*(0^2/2)+C_(2)*0+C_(3) ⇒ C_(3) =0
y`(0)=0 ⇒ 0=-sin0+C_(1)*0+C_(2) ⇒ C_(2) =0
y``(0)=0 ⇒ 0=-cos0+C_(1)⇒ C_(1) =1
---
y(x)= cosx+(x^2/2)
y(π/2)=cos(π/2)+(π^2/8) ≈ 0+(9,8596/8)=1,23
