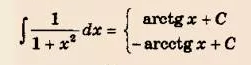Задача 41576 Решите дифференциальное уравнение с...

dasha288

2019-11-15 16:54:45

Решите дифференциальное уравнение с разделяющимися переменными.
(x+xy^2)dx+(1+x^2)dy=0

sova

2019-11-15 18:24:07

★

х*(1+y^2)dx=-(1+x^2)dy
Разделяем переменные.
Делим уравнение на
(1+y^2)*(1+x^2)

[m] \frac{xdx}{1+x^2}=- \frac{dy}{1+y^2}[/m]

Интегрируем:

[m]\int \frac{xdx}{1+x^2}=-\int \frac{dy}{1+y^2}[/m]

[m]\frac{1}{2}\cdot \int \frac{2xdx}{1+x^2}=-\int \frac{dy}{1+y^2}[/m]

[m]\frac{1}{2}\cdot \int \frac{d(1+x^2)}{1+x^2}=-\int \frac{dy}{1+y^2}[/m]

0,5ln(1+x^2)=arcctgy+ C - ответ