Задача 64047 2. Решение дифференциальных уравнений с...
Условие
2. Найти частные решения дифференциальных уравнений, удовлетворяющих начальным условиям: 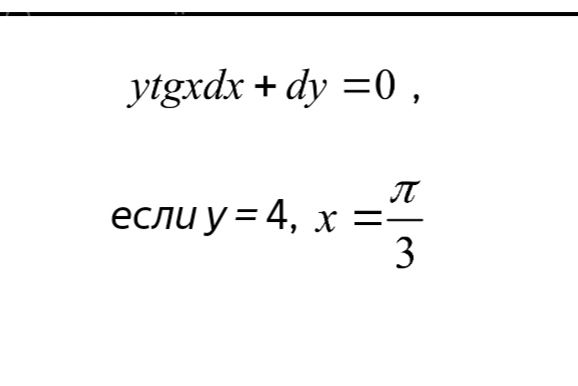
математика колледж
397
Решение
★
Разделяем переменные
tgxdx=-dy/y
-tgxdx=dy/y
Интегрируем
- ∫ tgxdx= ∫ dy/y
∫ d(cosx)/cosx= ∫ dy/y
[b]ln|cosx|+C=ln|y|[/b]- общее решение дифференциального уравнения
Находим частное решения , удовлетворяющее начальным условиям:
x=π/3; y=4
ln|cos(π/3)|+C=ln4
ln(1/2)+C=ln4
C=ln4-ln(1/2)
C=3ln2
[b]ln|cosx|+3 ln2=ln|y|[/b]-частное решение дифференциального уравнения
