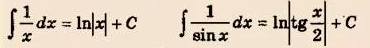Задача 59818 ...

60a5e09e3f1bb8747d24dbc5

20.05.2021 07:09:05

y'sinx-y ln y = 0,y (π/2)=1

5f3ea7e3faf909182968ddd9

20.05.2021 09:27:50

★

y'sinx–y ln y = 0,

y`=dy/dx

(sinx)*dy=(ylny)*dx - уравнение с разделяющимися переменными

dy/(ylny)=dx/(sinx)

∫ dy/(ylny)= ∫ dx/(sinx)

Так как d (lny)=(1/y)dy=dy/y, то

∫ d(lny)/(lny)= ∫ dx/(sinx)

cм скрин с формулами

ln|lny|=ln|tg(x/2)|+lnC

ln|lny|=lnC*|tg(x/2)|

lny=C*tg(x/2)

y=e^(C*tg(x/2))

y=e^(C)*e(tg(x/2))

e^(C) обозначим С

y=C*e^(tg(x/2))- [b]общее решение[/b]


Задача Коши:
y (π/2)=1


Подставляем
x=π/2
y=1
в общее решение и находим С

1=C*e^(tg(π/4))

1=C*e

C=1/e

y=(1/e)*e^(tg(x/2))- [b]частное решение[/b], удовлетворяющее условию y (π/2)=1


0=С*1