Задача 55976 Дифференциальные уравнения Буквы а, Б, г...
Условие
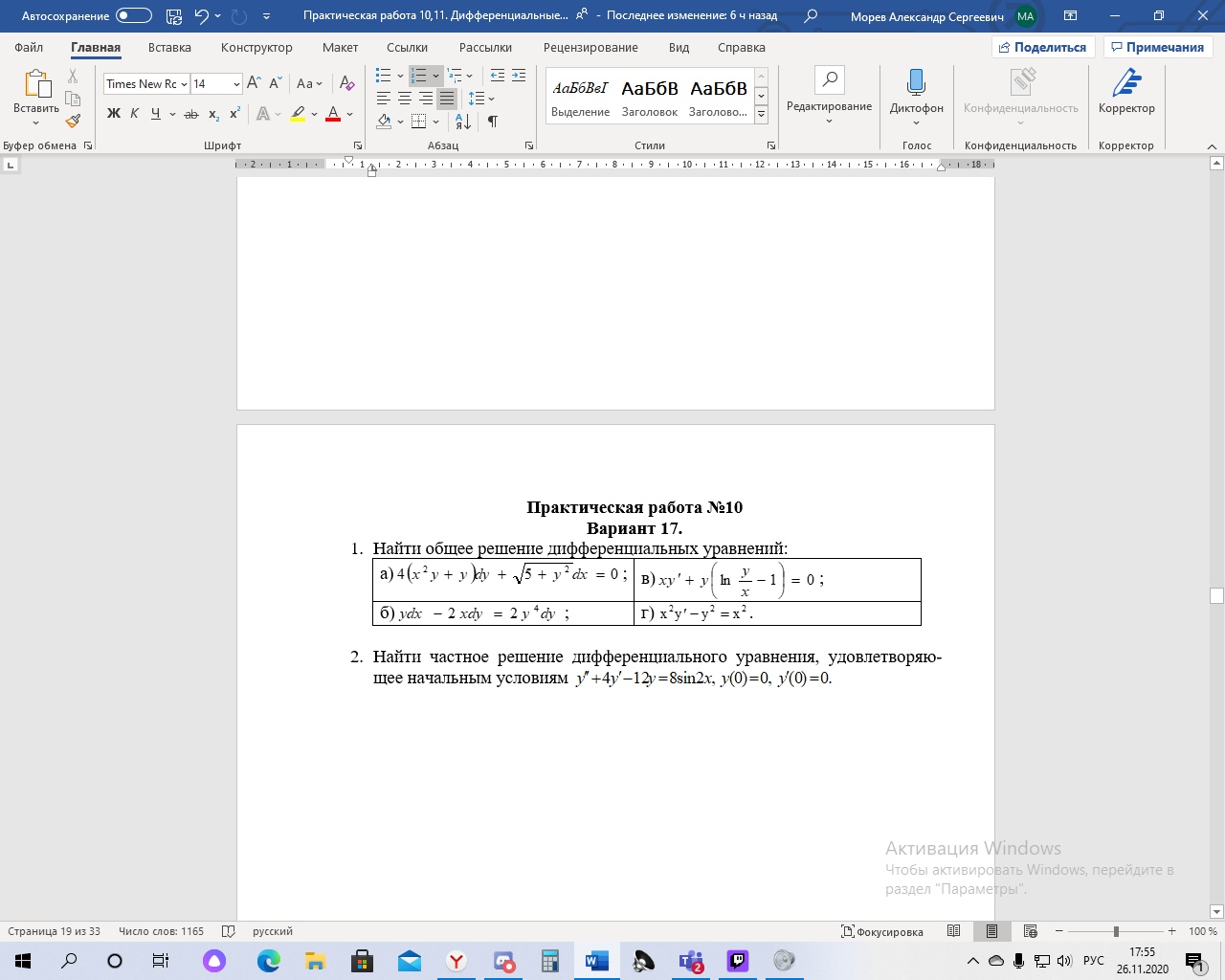
математика колледж
694
Решение
★
[m]4y⋅(x^2+1)dy=−\sqrt{5+y^2}dx[/m]
[m]\frac{4ydy}{\sqrt{5+y^2}}=-\frac{dx}{x^2+1}[/m]
Интегрируем и получаем ответ
г)
Делим на х^2
[m]y`–\frac{y^2}{x^2}=1[/m]
[m]\frac{y}{x}=u[/m] ⇒ [m]y=u\cdot x[/m]
⇒ [m]dy=udx+xdu[/m]
[m]udx+xdu=(u+1)dx[/m]
[m]xdu=(u+1–u)dx[/m]
[m]du=\frac{dx}{x}[/m]
[m]u=ln|x|+lnC[/m]
[m]u=lnCx[/m]
[m]y=x\cdot ln(Cx)[/m]
