Задача 60025 2. Найдите общее решение уравнения У`...

60b48c0ba1c50e1d3043892c

31.05.2021 10:13:13

2. Найдите общее решение уравнения У` -У`-6У70 . Изобразите интегральные кривые на плоскости

5f3ea7e3faf909182968ddd9

31.05.2021 12:08:27

★

Это линейное [b]однородное[/b] дифференциальное уравнение второго порядка с постоянными коэффициентами.

Составляем характеристическое уравнение:
k^2-5k-6=0
D=25+24=49=7^2

k_(1)=-1 и k_(2)=6 - корни действительные различные,


поэтому [b]общее решение однородного уравнения[/b] с постоянными коэффициентами имеет вид:

y_(общее одн)=C_(1)e^(k_(1)x)+C_(2)e^(k_(2)x) - общее решение однородного уравнения

k_(1)=-1 и k_(2)=6

y_(общее одн)=C_(1)e^(-x)+C_(2)e^(6x)

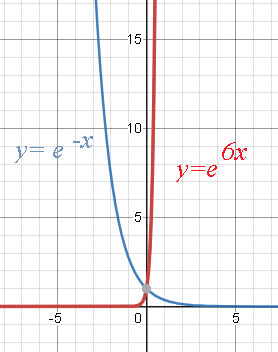
Графики

y=e(-x)

y=e^(6x)

на рисунке

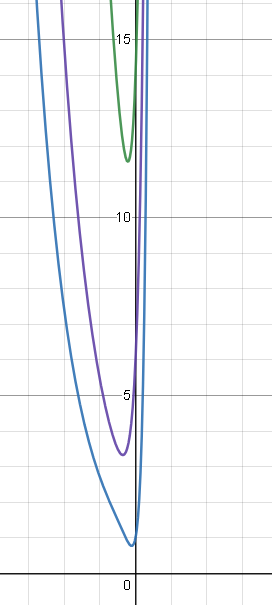
Интегральные кривые, это кривые вида y=C_(1)e^(-x)+C_(2)e^(6x) при различных значениях С_(1) и С_(2)

Например, такие: