Задача 35048 Найдите общее решение дифференциального...

vk459344689

2019-03-27 23:02:19

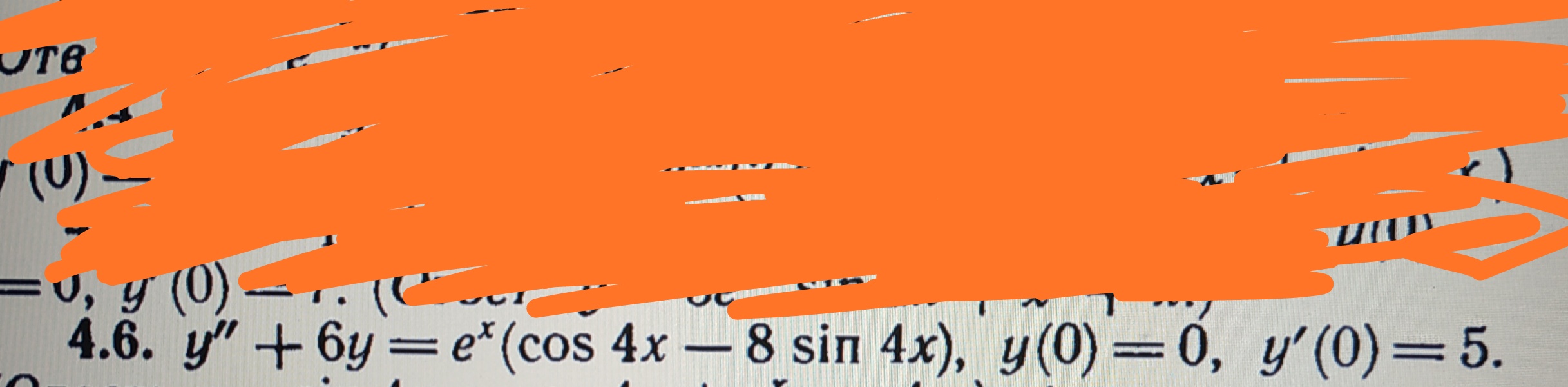
Найдите общее решение дифференциального уравнения

sova

2019-03-28 13:24:01

★

Линейное неоднородное уравнение второго порядка с постоянными коэффициентами.

Составляем характеристическое уравнение:
k^2+6=0

k1=-sqrt(6)*i; k2=sqrt(6)i– корни комплексно-сопряженные

α =0 β=sqrt(6)

Общее решение однородного уравнения имеет вид:
y_(одн.)=С_(1)*cossqrt(6)x+C_(2)sinsqrt(6)x

частное решение неоднородного уравнение находим в виде:
y_(част)=e^(х)*(Asin4x+Bcos4x)


Находим производную первого, второго порядка

y`_(част)=e^(x)*(Asin4x+Bcos4x)+e^(x)*(4Acos4x-4Bsin4x)

y`_(част)=e^(x)*(Asin4x+Bcos4x+ 4Acosx-4Bsinx)


y``_(част)=e^(x)(Asin4x+Bcos4x+ 4Acos4x-4Bsin4x)+e^(x)*(4Acos4x-4Bsin4x-16Asin4x-16Bcos4x)

y``_(част)=e^(x)(Asin4x+Bcos4x+ 4Acos4x-4Bsin4x+4Acos4x-4Bsin4x-16Asin4x-16Bcos4x)

подставляем в данное уравнение:

e^(x)(Asin4x+Bcos4x+ 4Acos4x-4Bsin4x+4Acos4x-4Bsin4x-16Asin4x-16Bcos4x)+6*e^(х)*(Asin4x+Bcos4x)=e^(x)*(cos4x-8sin4x)

e^(x)(Asin4x+Bcos4x+ 4Acos4x-4Bsin4x+4Acos4x-4Bsin4x-16Asin4x-16Bcos4x+6Asin4x+6Bcos4x)=e^(x)*(cos4x-8sin4x)

Asin4x-4Bsin4x-4Bsin4x-16Asinx+6Asin4x=-8sin4x
Bcos4x+ 4Acos4x+4Acos4x-16Bcos4x+6Bcos4x)=cos4x

Cистема:
{A-4B-4B-16A+6A=-8
{B+4A+4A-16B+6B=1

{9A+8B=8
{8A-9B=1

A=80/145=16/29
B=11/29
y_(част)=e^(х)*((16/29)*sin4x+(11/29)*cos4x)

О т в е т.
Общее решение :
у=y_(одн.)+y_(част)=С_(1)*cossqrt(6)x+C_(2)sinsqrt(6)x+e^(х)*((16/29)*sin4x+(11/29)*cos4x)