Задача 66425 Найти общее решение ДУ: y'+4y/x =...
Условие
y'' - 9y' = 3x^2+3x+1
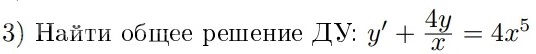
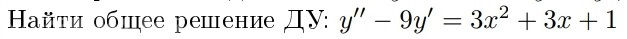
Решение
Линейное
y=u*v
y`=u`*v+u*v`
u`*v+u*v`+(4/x)*u*v=4x^5
Группируем
u`*v+u*(v`+(4/x)*v)=4x^5
Условия на функцию v ( пусть выражение в скобках равно 0)
v`+(4/x)*v=0
тогда
u`*v=4x^5
Решаем первое уравнение с разделяющимися переменными
v`+(4/x)*v=0
dv/v=-4dx/x ⇒ ∫ dv/v=-4 ∫ dx/x
lnv=-4lnx
lnv=lnx^(-4)
lnv=ln(1/x^4)
v=1/x^4
Подставляем во второе
u`*v=4x^5
u`*(1/x^4)=4x^5
u`=4x^9
u=5x^(10)/10+C
y=u*v=((1/2)x^(10)+C)*1/x^4
[b]y=(1/2)x^6+(C/x^4)[/b]
Второе уравнение - линейное [b]неоднородное[/b] дифференциальное уравнение второго порядка с постоянными коэффициентами
Решаем [i]однородное[/i] дифференциальное уравнение второго порядка с постоянными коэффициентами
y`` - 9y` =0
Составляем характеристическое уравнение:
k^2-9k=0
k*(k-9)=0
k=0; k=9- корни характеристического уравнения , действительные различные.
В этом случае общее решение имеет вид:
y=C_(1)*e^(0x)+C_(2)*e^(9x)
[b]y=C_(1)+C_(2)*e^(9x)[/b] - общее решение уравнения y`` -9y` =0
Частное решение находим в виде, который зависит от правой части и корней характеристического уравнения
y_(частное неодн)=х*(Ax^2+Bx+C) или y_(частное неодн)=Ax^3+Bx^2+Cx
Находим производные:
y`_(частное неодн)=Ax^3+Bx^2+Cx
y``_(частное неодн)=Ax^3+Bx^2+Cx
Подставляем в данное уравнение и [b]находим А. В. С[/b]
и тогда
y_(общее неодн)=y_(общее одн)+y_(частное неодн)=C_(1)+C_(2)*e^(9x)+Ax^3+Bx^2+Cx
