Задача 60236 5y'' 6y' + 5y =e^(0,6x) sin 0,8x. ЛНДУ...
Условие
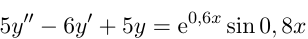
Решение
Решаем однородное :
5y'' − 6y' + 5y =0
Составляем характеристическое уравнение:
5k^2-6k+5=0
D=36-4*5*5=-64
k_(1)=(6-8i)/10; k_(2)=(6+8i)/10– корни комплексно-сопряженные
k_(1)=0,6-0,8i; k_(2)=0,6+0,8i– корни комплексно-сопряженные
α =0,6 ; β=0,8
Общее решение однородного уравнения имеет вид:
y_(общее одн.)=e^(αx)*(С_(1)*cos βx+C_(2)*sin βx)
Применяем метод неопределенных коэффициентов, так как правая часть уравнения имеет специальный вид.
Частное решение неоднородного уравнение находим в виде:
y_(част неод)=[b]x[/b]*e^(0,6х)*(Acos0,8x+Bsin0,8x)
Находим производную первого, второго порядка
y`_(част неод)=
y``_(част неод)=
подставляем в данное уравнение:
и находим коэффициенты:
A=-1/8
B=0
О т в е т.
Общее решение :
у_(общее неод)=y_(обще одн.)+y_(част неод)=e^(αx)*(С_(1)*cos βx+C_(2)*sin βx)+[b]x[/b]*e^(0,6х)*(-1/8)*cos0,8x
