Задача 71591 Решите дифференциальное уравнение y'' -...
Условие
y'' - 2y' + y = e^x / (x^2+1), y(0) = 0, y'(0) = 0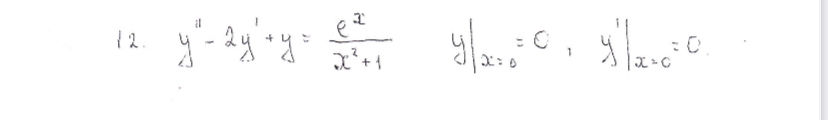
Решение
y``-2y`+y=0
Составим характеристическое уравнение:
k²-2k+1=0 ;
k_(1)=k_(2)=1- корни действительные кратные
y_(однород)=C_(1)e^(x)+C_(2)*x*e^(x)
Применяем метод вариации произвольных постоянных
Для этого константы С_(1) и С_(2) считаем зависящими от х
[b]y=C_(1)(х)*e^(x)+C_(2)(х)*x*e^(x) (#)[/b]
C_(1) x и С_(2)(х) находим из системы:
{ C’_(1)(x)*e^(x)+C`_(2)(x)*x*e^(x)=0;
{C`_(1)(x)*(e^(x))`+C’_(2)(x)(x*e^(x))`=e^(x)/(x^2+1)
{ C’_(1)(x)+C`_(2)(x)*x=0 ⇒ C’_(1)(x)=-C`_(2)(x)*x и подставляем во второе:
{C`_(1)(x)*e^(x)+C’_(2)(x)(e^(x)+x*e^(x))=e^(x)/(x^2+1)
{ C’_(1)(x)=-C`_(2)(x)*x
{-C`_(2)(x)*x *e^(x)+C’_(2)(x)(e^(x)+x*e^(x))=e^(x)/(x^2+1) ⇒ С`_(2)(x)=1/(x^2+1) ⇒ C_(2)(x)= ∫dx/(x^2+1) =arctgx+C_(2)
C`_(1)(x)=-(arctgx+C_(2))*x
C_(1)(x)= ∫ (-(arctgx+C_(2))*x)dx=- ∫ x*arctgxdx+C_(2) ∫ xdx=
u=arctgx
dv=xdx
du=dx/(x^2+1)
v=(x^2/2)
C_(1)(x)= ∫ (-(arctgx+C_(2))*x)dx=- (x^2/2)*arctgx+(1/2) ∫x^2/(x^2+1)dx +C_(2) ∫ xdx=- (x^2/2)*arctgx+(1/2)x-(1/2)arctgx+C_(2)*(x^2/2)+C_(1)
Подставляем в
[b]y=C_(1)(х)*e^(x)+C_(2)(х)*x*e^(x) (#)[/b]
y=(- (x^2/2)*arctgx+(1/2)x-(1/2)arctgx+C_(2)*(x^2/2)+C_(1))*e^(x)+(arctgx+C_(2))*x*e^(x)
y(0)=0
⇒
0=C_(1))*e^(0) ⇒ C_(1)=0
y`(0)=0
y`=((- (x^2/2)*arctgx+(1/2)x-(1/2)arctgx+C_(2)*(x^2/2)+C_(1))*e^(x)+(arctgx+C_(2))*x*e^(x))`
считайте производную.
