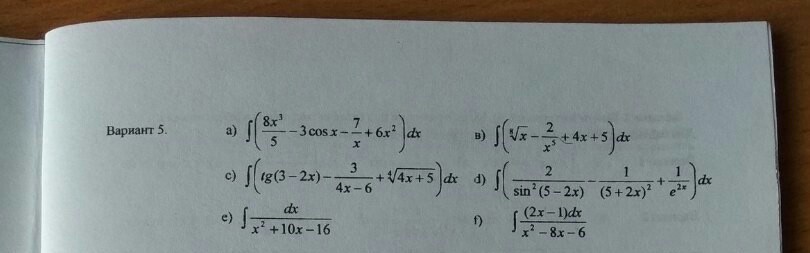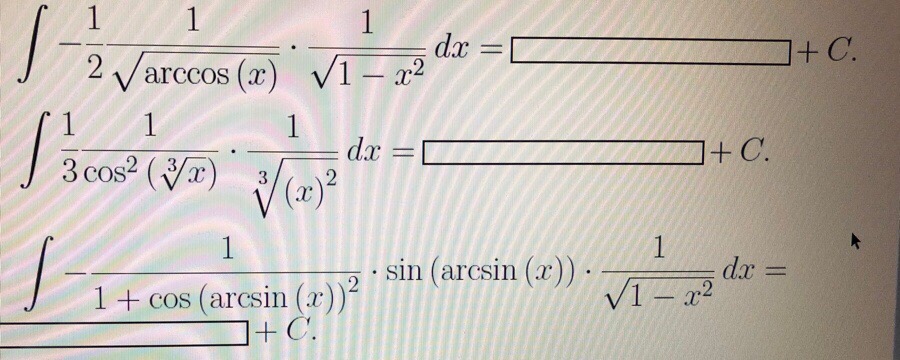Непосредственное интегрирование

Добрый день решите интегралы, большое спасибо.

3 X +x J.4—dx. 2.13. ° X +1 хелп

Здравствуйте, можете помочь решить пример, буду благодарен. Спасибо!
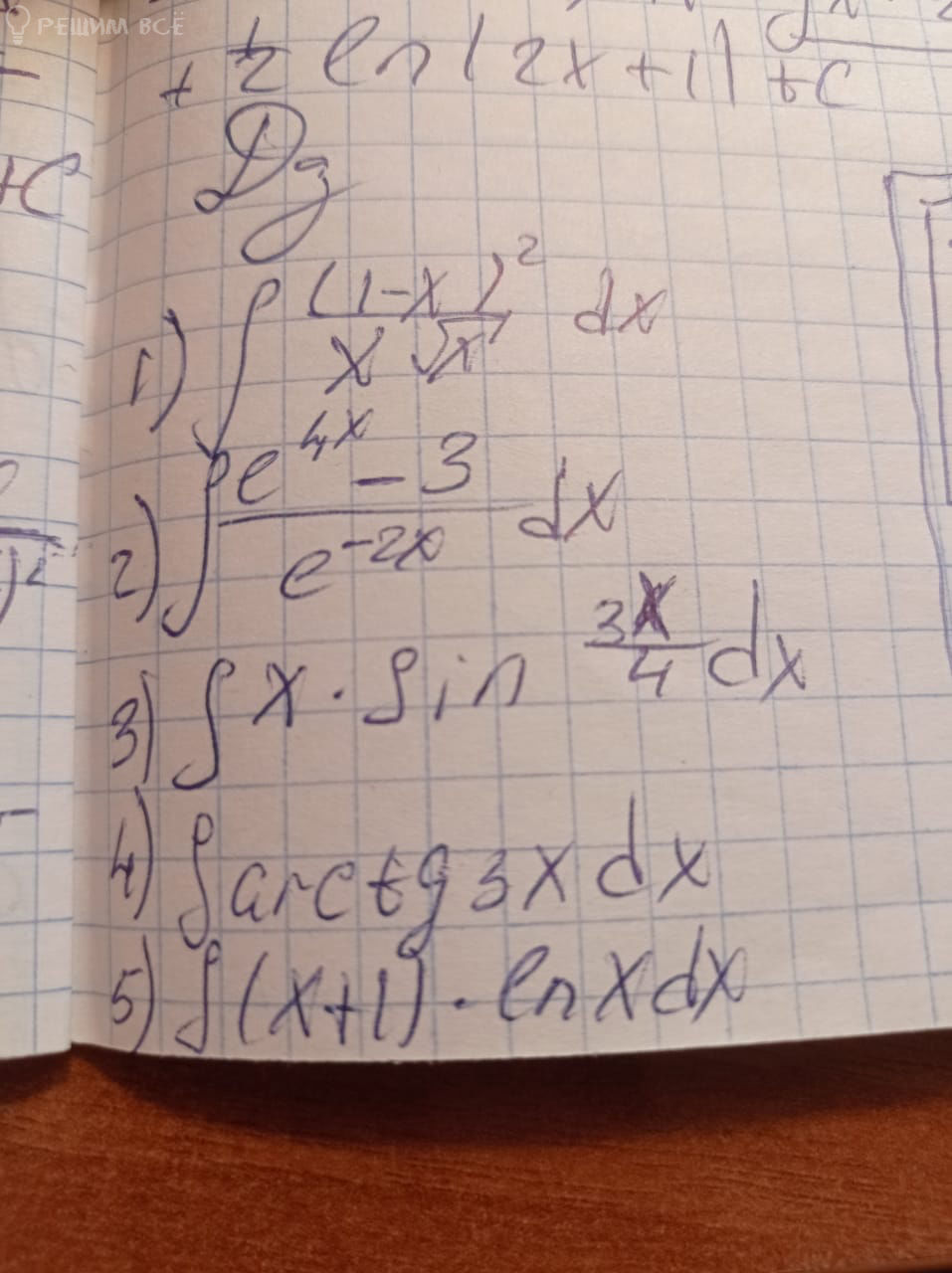
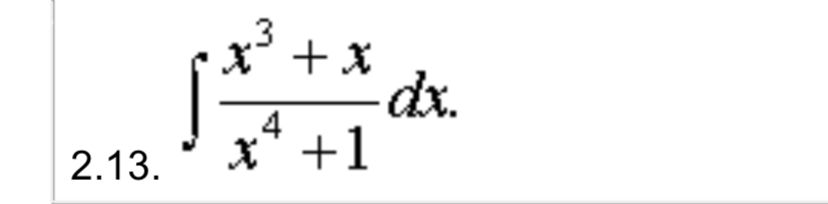
Тема: Интегралы

Решить неопределённый интеграл:
∫ [m]\frac{1}{\sqrt{x^2+1}-\sqrt{x^2-1}}{dx}[/m]

Вычислить интегралы:

Вычислить неопределенный интеграл

Решить неопределенные интегралы

Пожалуйста помогите решить примеры от 1 до 5

7. Найти интеграл ∫ (2e^x - 3 sinx + 5) dx

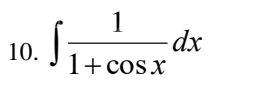
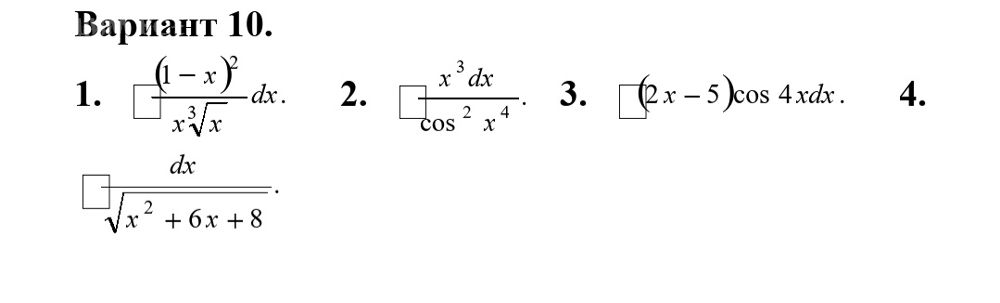
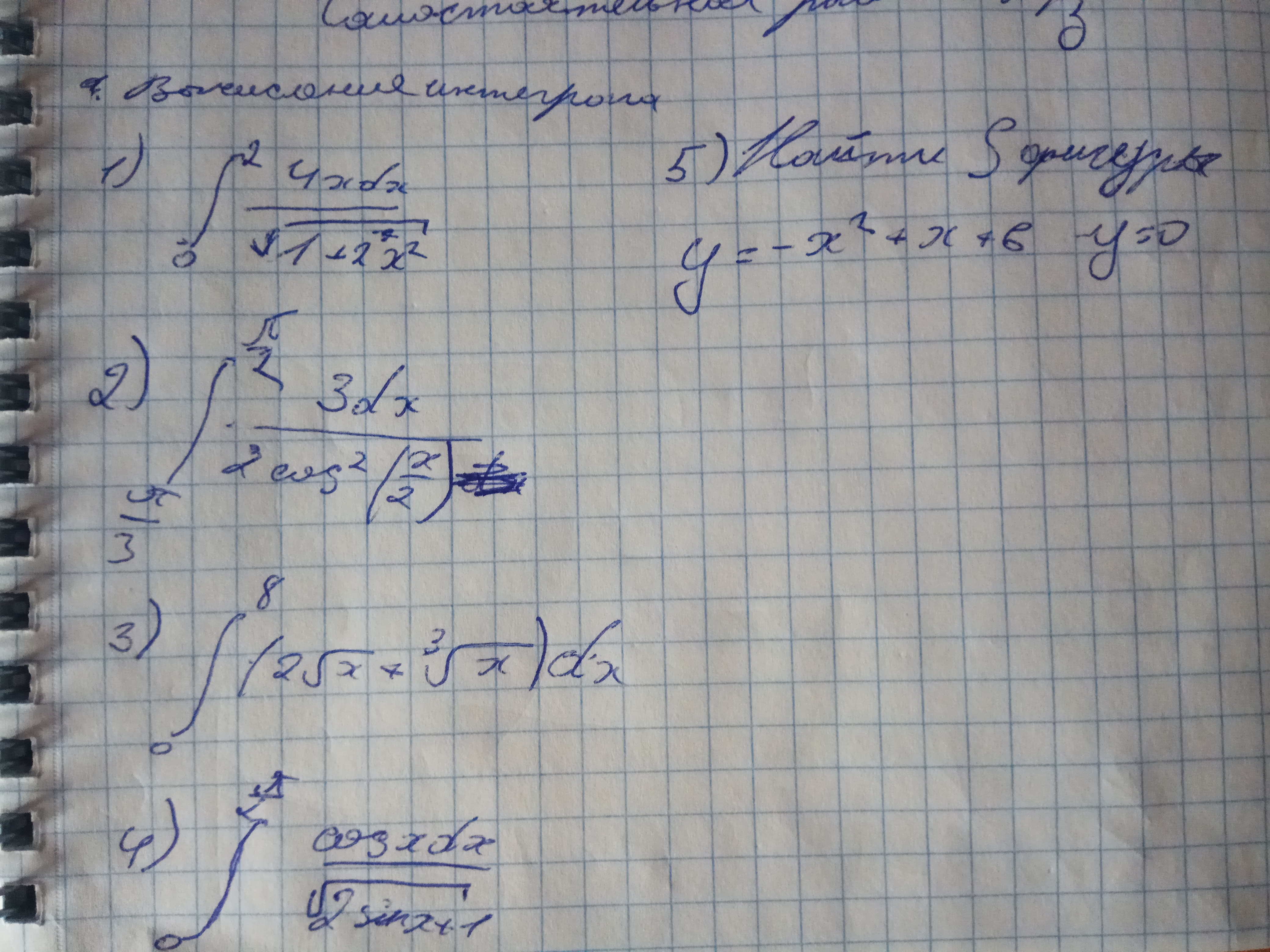
8. Найти интеграл ∫ from -1 to 1 e^(2x+1) dx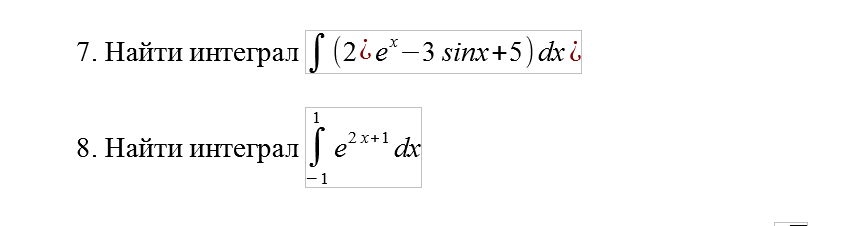

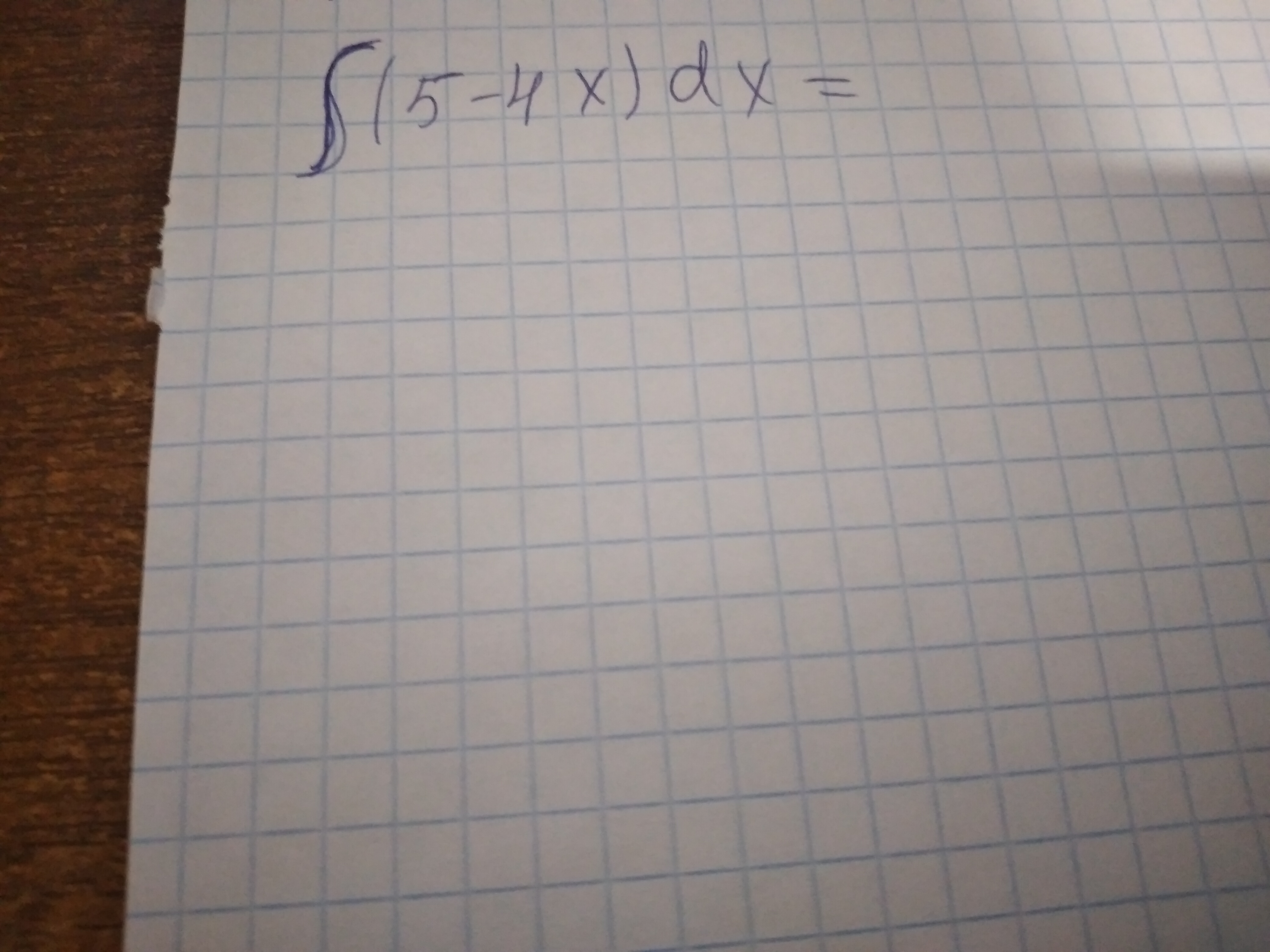
Найдите общий видпервообразных для фукций

∫ (5-4x)dx

Найти неопределённые интегралы и полученные результаты проверить дифференцированием

Помогите решить ,желательно подробно ,хочу разобраться в решении

5) ∫ 4dx / (1 - 3x)^5;
6) ∫ sin 2x dx.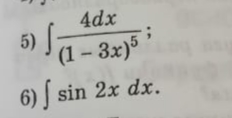

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

Укажите все верные утверждения

8.1.2. ∫ x^10 dx.
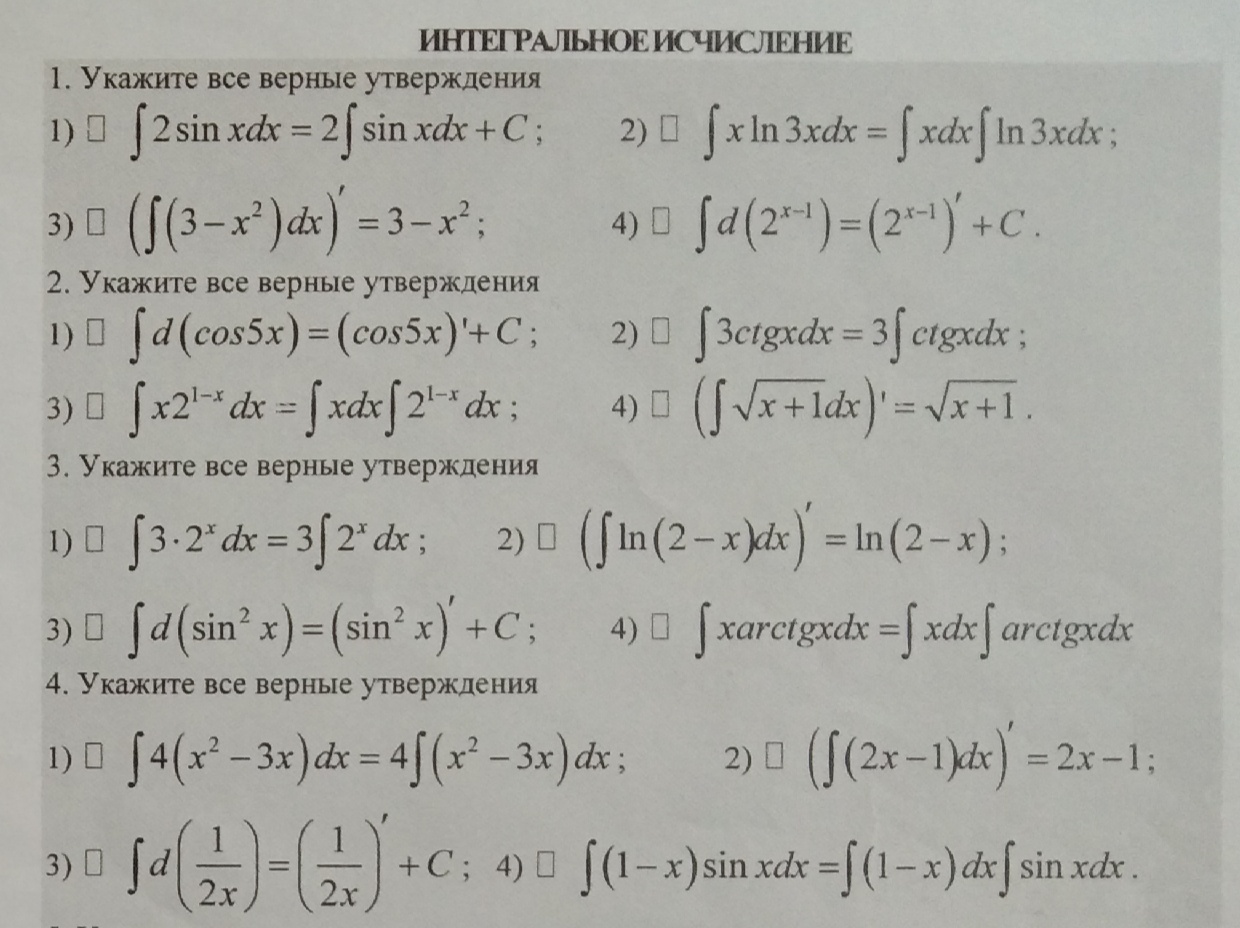
8.1.4. ∫ 4√x dx.
8.1.6. ∫ dx / (x^2 - 1/2)

8.1.3. ∫ dx / x.
8.1.5. ∫ dx / (x^2 + 9)
8.1.7. ∫ dx / √(x^2 + 3)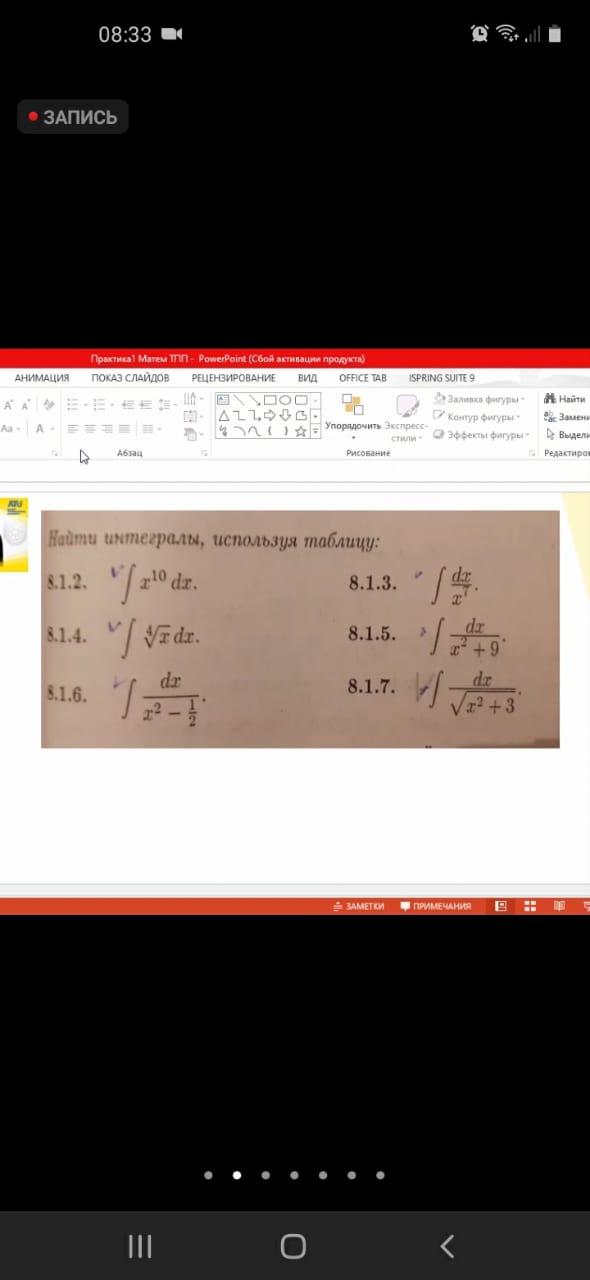

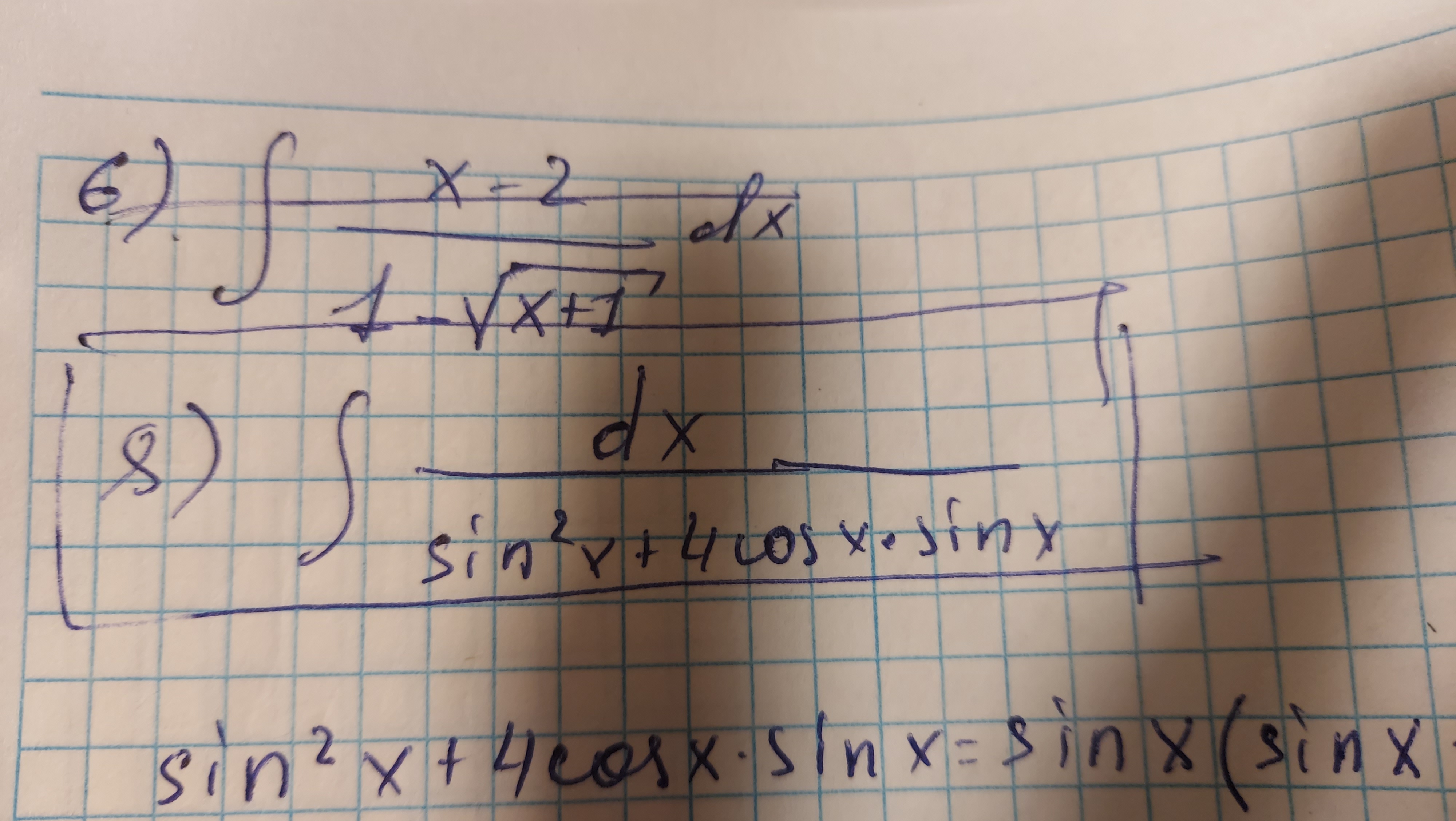
Нужен решить интеграл

Вычислите неопределенные интегралы

1. ∫ ( (4/3) x^3 - (3/4) x^2 + 5 ) dx

Вычислите неопределенные интегралы

2. ∫x³(1 + 5x)dx

Вычислите неопределенные интегралы

3. ∫ (3^x - e^x + 2x - 1) dx

Вычислите неопределенные интегралы

4. ∫ (5x + 3)³ dx

Вычислите неопределенные интегралы

5. ∫(x^(-4) - x^(-3) - 3x^(-2) + 1) dx

Вычислите неопределенные интегралы

∫ (5x⁴ dx) / (x⁵ + 9)

∫ = tg³x/cos²x dx

∫ 3dx / (4 - 5x)

Помогите пожалуйста

Решить интегралы ∫ dx/(sqrt(8x^2-2) и остальные...

26. a) ∫(√(3 - x) + √(3 + x)) / √(9 - x^2) dx ; б) ∫(x^2 - 6)*3^x dx ;
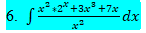
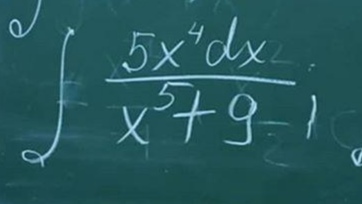
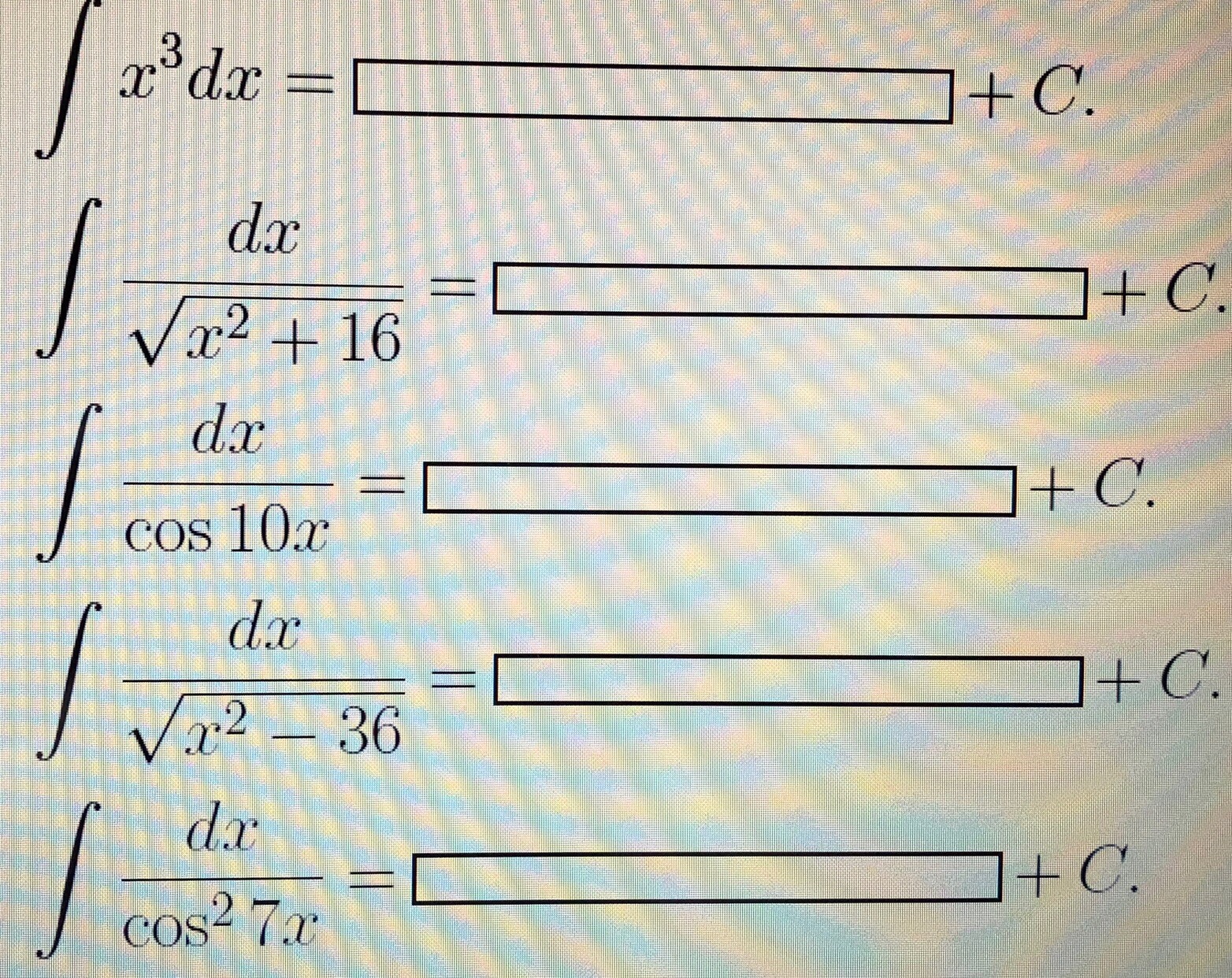
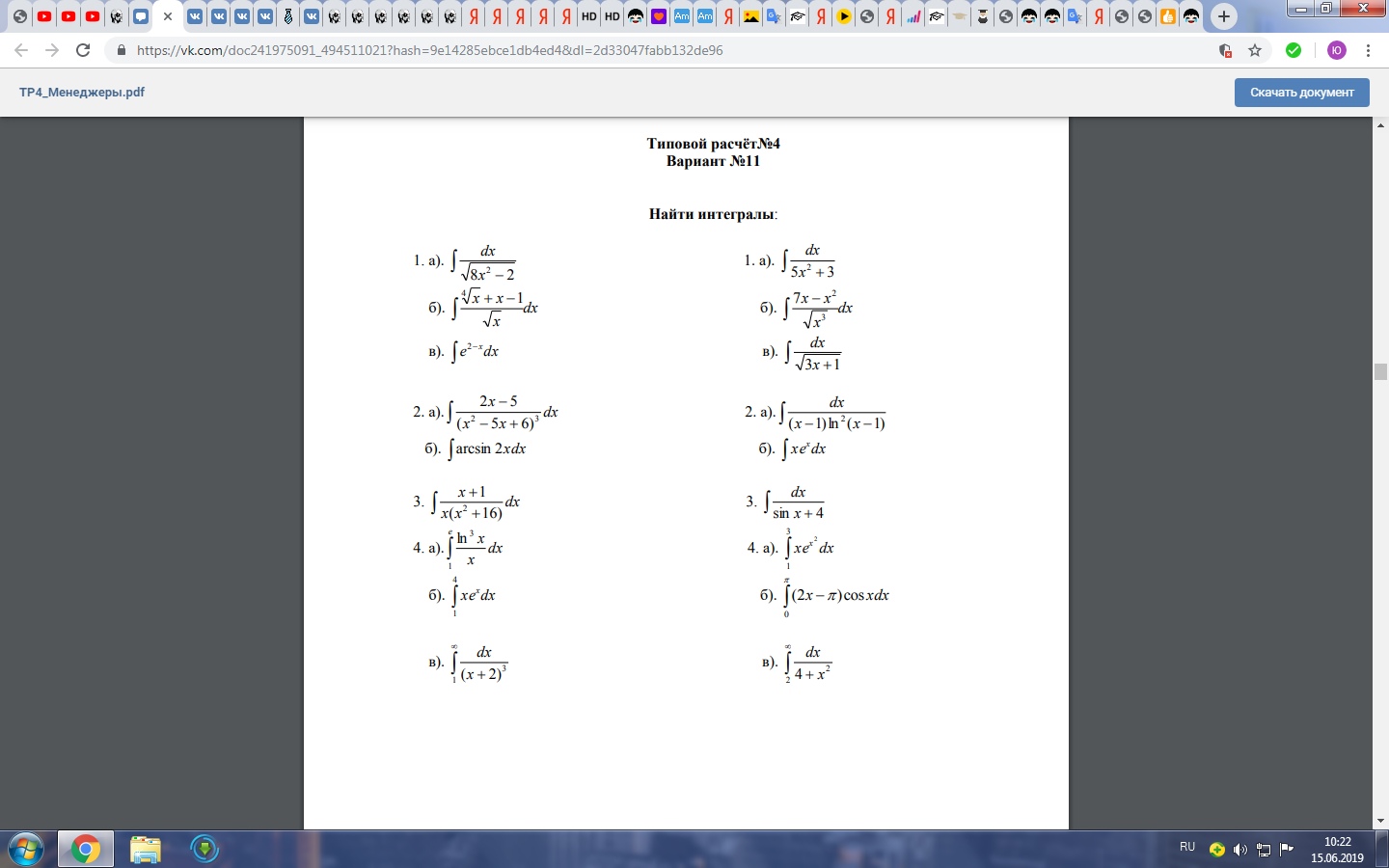
в) ∫(4x^3 + 2x^2 + 1) / x(x - 1)^2 dx ; Г) ∫(1 / (2 + 5cos^2x)) dx ; Д)

∫(4x + 3) / √(7 - 2x - x^2) dx.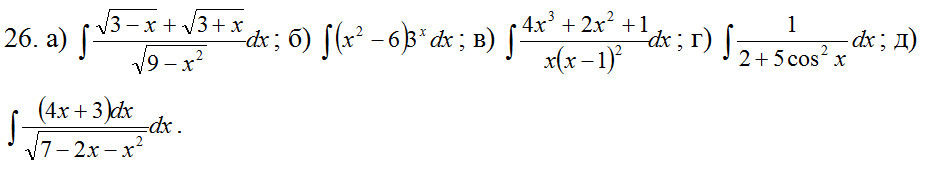

Пятое задание (Найдите неопределённые интегралы) под з, м, т

∫ (3^x/ sqrt(9^x-10)dx

xdx/ sqrt(3x^2+8)

∫ x^(4) / x^(2) - 1 dx

Нужна помощь с интегралами.

Решить интегралы.3,7,8,9,10

помогите, пожалйста, решить.
1.Найдите неопределенные интегралы:
а) ∫▒(2/√х- (4√(3&x^2 ))/х)dx ; б)∫▒xdx/(〖sin〗^2 (x^2 ) ̇ )
2.Найдите определенные интегралы:
а)∫_(√5)^(2√2)▒xdx/√(3x^2+1); б)∫_0^(π/6)▒〖e^sin⁡x cos⁡xdx 〗

Решить интеграл
sqrt(подкоренное выражение)(1+sin2x)dx

Задание№1 Вычислить интегралы a) ∫ sin(3x-п/3)Умножить на dx
б)
25
∫ (1/sqrt(x) -1) умножить на dx
9
в) ∫ x/7+x^(2) dx (замена t=7+x^(2))

умоляю помогите решить

∫( 1 + x^2 )^(-1)
-----------------------
arctg x - 10 dx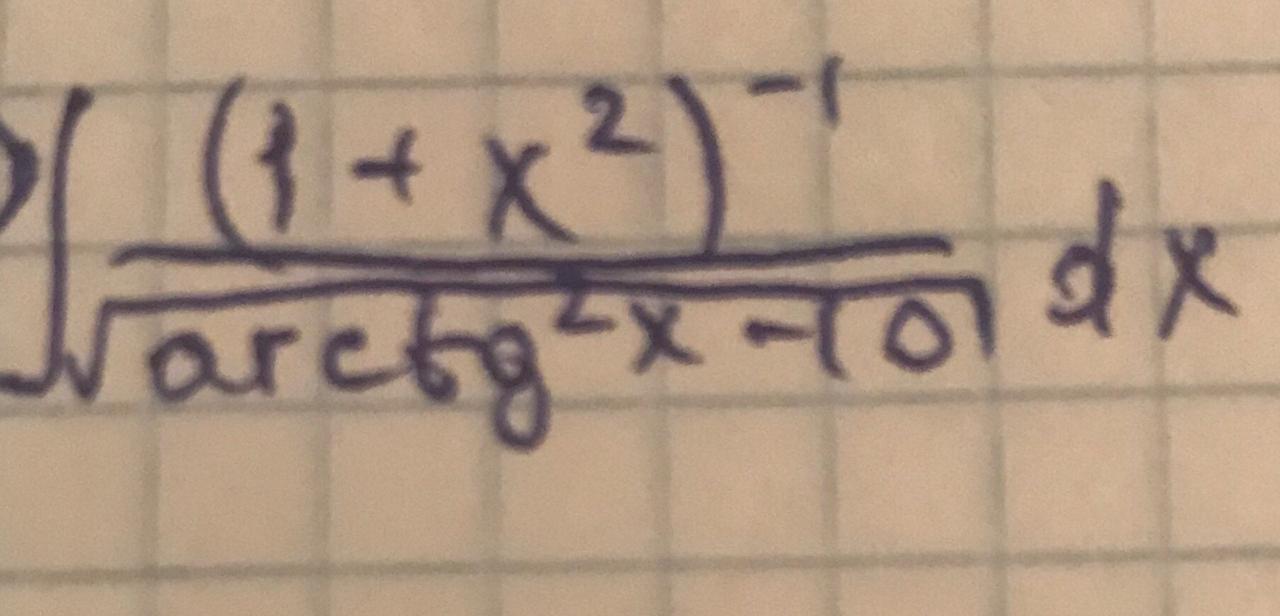

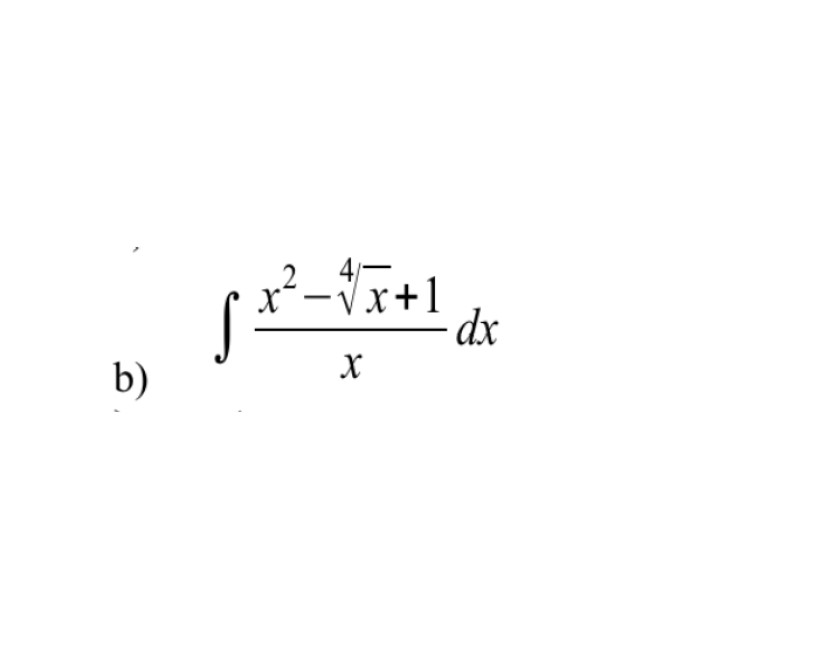
найти не определенные интегралы

23 задача Найти неопределенные интегралы

Вариант 7.

1) ∫(4 - x^7 + 1/x^7) dx;

2) ∫ (9x - 3/x^4 + 2x^5) dx;

3) ∫(6x^11 + 4x - 1) dx;

4) ∫(7x - 3)^3 dx;

5) ∫ 12dx/(4 - 6x)^5;

6) ∫ sin 3x dx.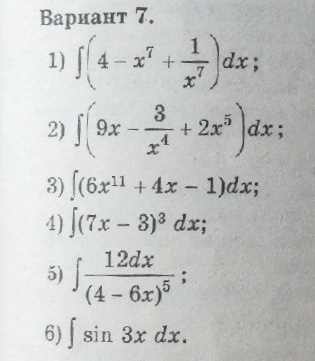

Найти интеграл
∫(cos7x+((5xe^x-2)/x))dx

∫ sqrt(2dx)/ sqrt(7-2x^(2))

dx/3x^(2)-5

∫ (sin4x) / (3√(cos²4x)) dx

Решить задание под буквой А И В 1 варианта
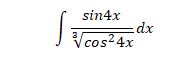
Решить неопределенный интеграл и выполнить проверку дифференцированием

Пожалуйста решите

1. ∫ xdx / √(1 - x²)

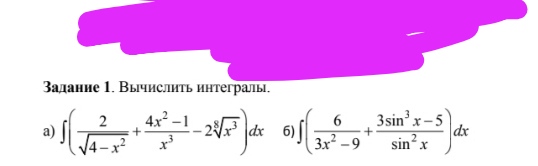
2. ∫(1 + 2x)cos x dx

3. ∫ (x⁵ + x⁴ - 8) / (x³ - 4x) dx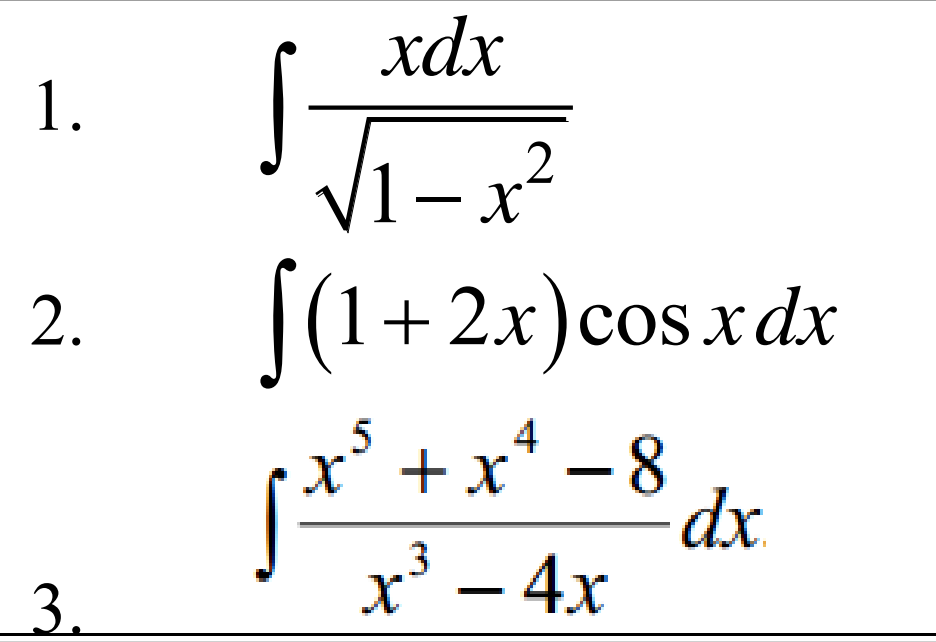

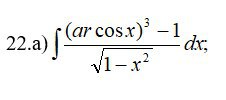
22. a) ∫(arc cos x)^3 - 1 / √1 - x^2 dx,

Задание на картинке

Вычислите интегралы

∫ (6x² + 16x - 1,5) dx

Вычислите интегралы

∫ cos(5x + 7) dx

Вычислите интегралы

∫ x^(1/3) dx

Вычислите интегралы

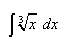
∫ (1 + x + x² + x³) dx

Решить интеграл
Dx/(x(5+ln^2x)

Решить интеграл
(2^(2х)-1)/sqrt(2^x)

Решить интеграл
dx(2x-(arcsinx)^(1/2))/(1-x^2)^(1/2)

∫ cossqrt(x) dx/(2sqrt(x)

∫ sin3xdx/sqrt(5+cos3x)

...

1681. ∫(dx / 2√x)

Здравствуйте пожалуйста решите интегралов
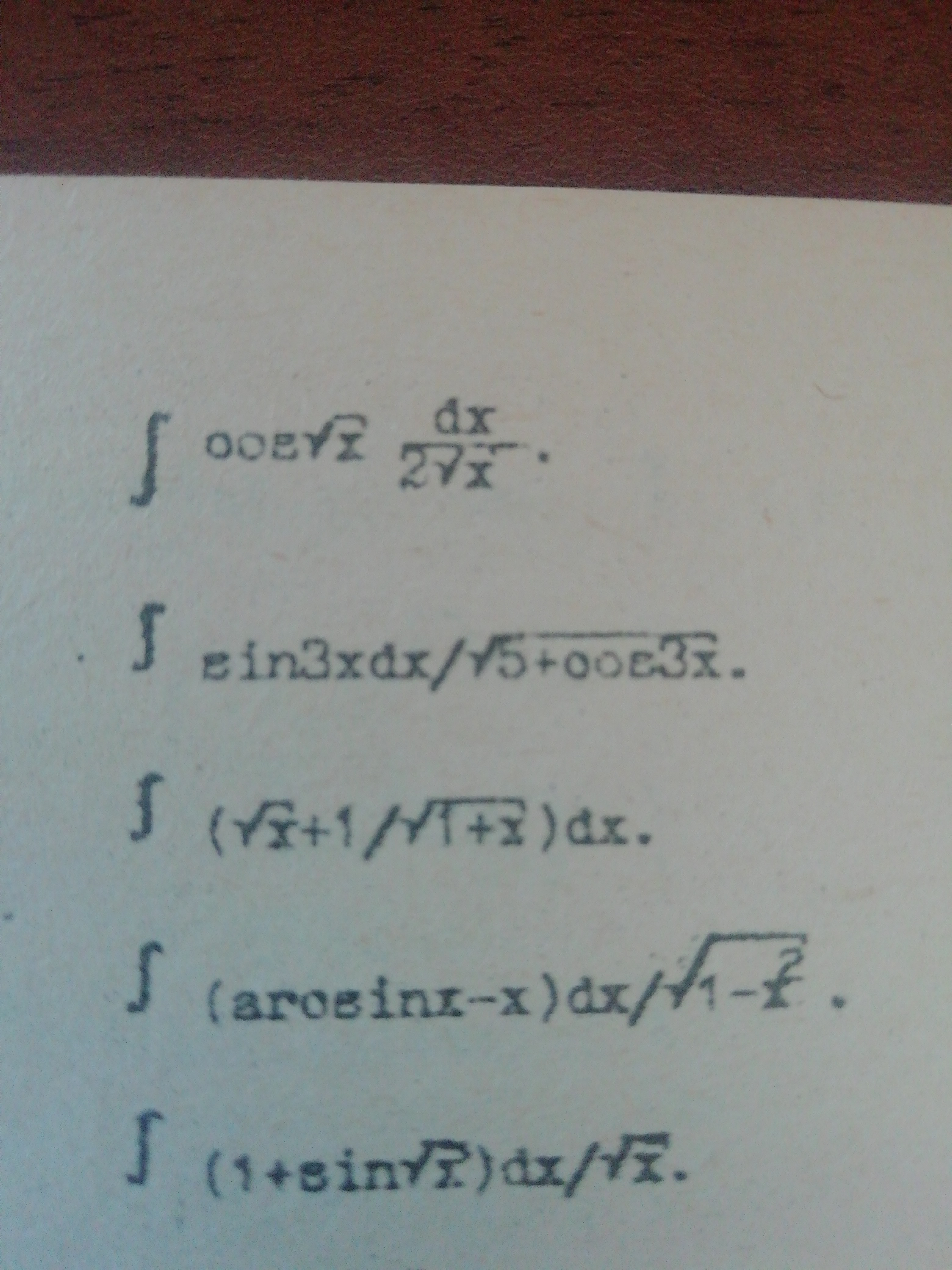
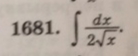
Опишите по шагам решение

1685. ∫ (√x + 1)(x - √x + 1) dx.

1687. ∫ (2x⁻¹.² + 3x⁻⁰.³ - 5x⁰.³⁸) dx.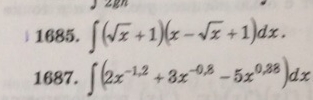

1. ....
2. ∫ sin(1-x^2)x dx
3. ∫ e^x dx / (4+e^(2x))
...

∫ (1+3x)/( sqrt(1+4x^(2))dx
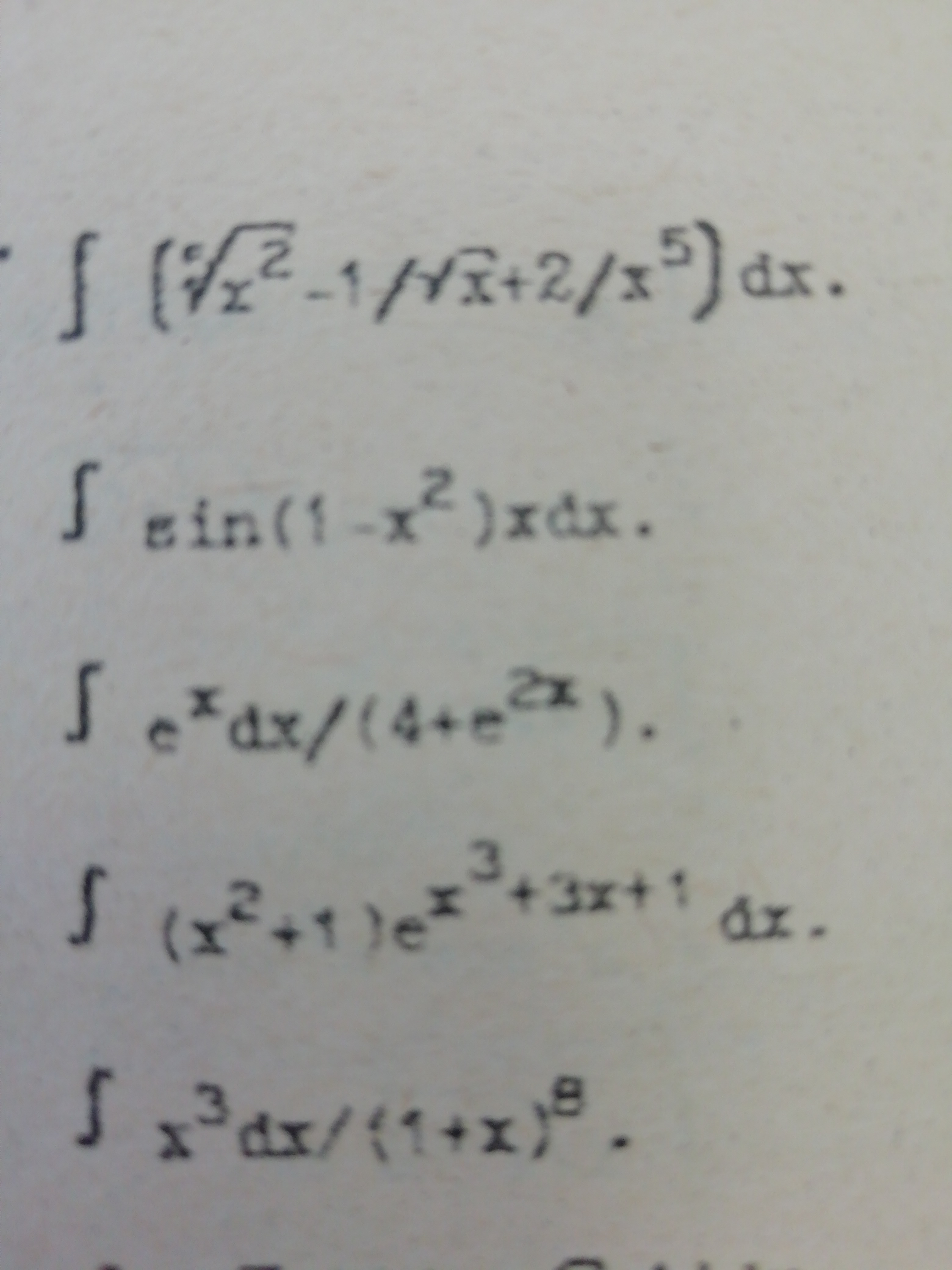
Решите пожалуйста!!

1, 2 , 4 , 5

❤