Задача 33497 Решить интегралы.3,7,8,9,10...
Условие
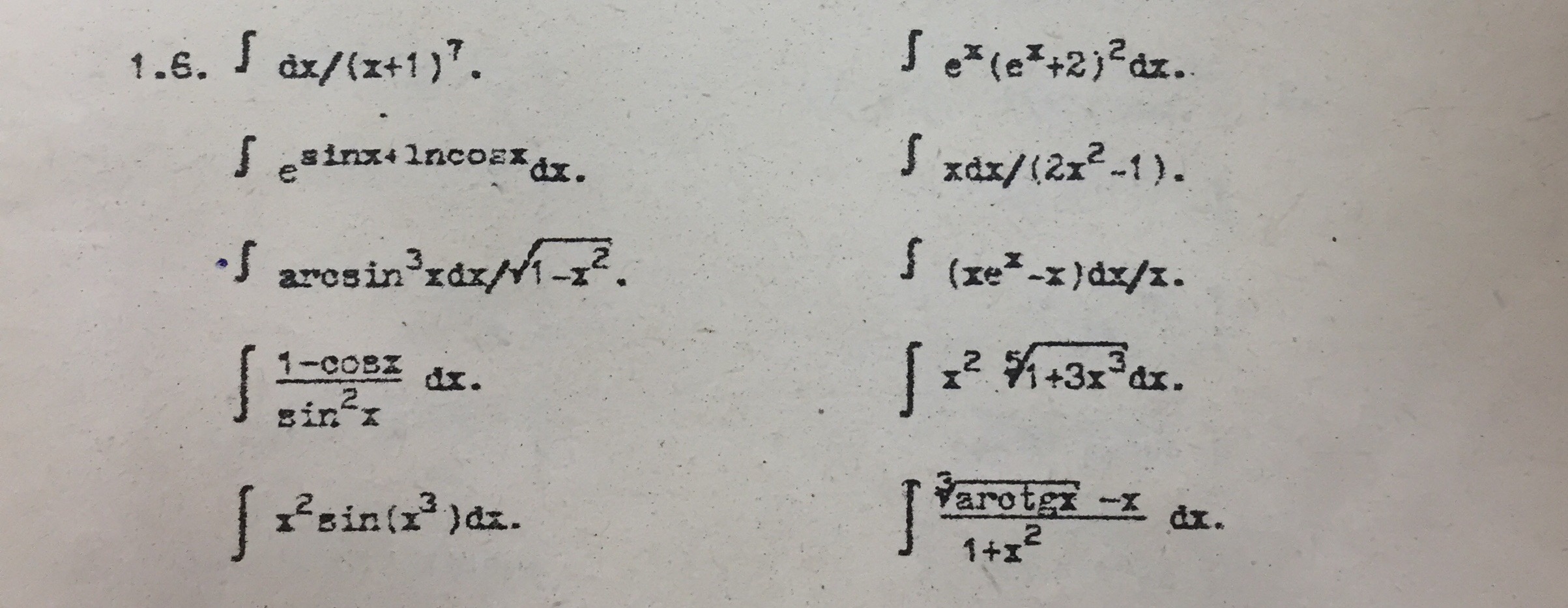
Решение
Замена переменной
u=arcsinx
du=dx/sqrt(1-x^2)
Получаем
∫ u^3/du=u^4/4=(arcsin^4x)/4+C
Можно сразу без замены писать:
∫ arcsin^3xdx/sqrt(1-x^2)= ∫ arcsin^3xd(arcsinx)=(arcsin^4x)/4 + C
7.
∫ xdx/(2x^2-1)
u=2x^2-1
du=4xdx
xdx=(1/4)du
получаем
∫ (1/4)du/u=(1/4) ∫ du/u=(1/4)ln|2x^2-1|+C
8.
(xe^(x)-x)/x=x*(e^(x)-1)/x=e^(x)-1
получаем
∫ (e^(x)-1)dx= ∫ e^(x)dx- ∫ dx=e^(x)-x + C
9.
u=1+3x^3
du=9x^2dx
x^2dx=(1/9)du
получаем
∫ (1/9)u^(1/5)du= (1/9)*u^((1/5)+1)/((1/5)+1)=(5/54)u^(6/5)+C=
=(5/54)*(1+3x^3)^(6/5) + C
10.
Интеграл от суммы (разности) равен сумме (разности) интегралов
получаем
∫ ∛arctgxdx/(1+x^2) - ∫ xdx/(1+x^2)=
= ∫ ∛u du - (1/2) ∫ dt/t=
=(3/4)(arctgx)^(4/3) - (1/2) ln (1+x^2) + C
