Задача 35542 ...
Условие
1) ∫(4 - x^7 + 1/x^7) dx;
2) ∫ (9x - 3/x^4 + 2x^5) dx;
3) ∫(6x^11 + 4x - 1) dx;
4) ∫(7x - 3)^3 dx;
5) ∫ 12dx/(4 - 6x)^5;
6) ∫ sin 3x dx.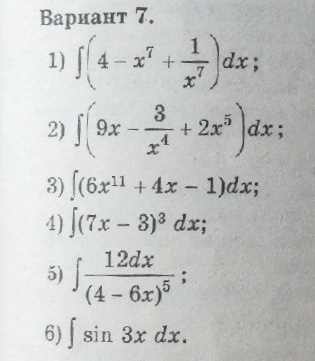
Решение
∫ (4-x^7+x^(-7))dx= 4x - x^(8)/8 +x^(-6)/(-6) + C=4x-(1/8)x^(8)-(1/6)*(1/x^6)+C
2)
1)
∫ (9x-3x^(-4)+2x^(5))dx= (9x^2/2) -3*x^(-3)/(-3) +2x^(6)/(6) + C=
=(9/2)x^2+(1/x^(3))+(1/3)*x^6+C
3)
∫ (6x^(11)+4x-1)dx=6*x^(12)/12 +4*(x^2/2)-x +C=(1/2)*x^(12)+2*x^2-x+C
в 4); 5); 6) применяем метод подведения под дифференциал.
(см. приложение)
4)
∫ (7x-3)^3dx=(1/7) ∫ (7x-3)^3d(7x-3)=(1/7)*((7x-3)^4/4)+C=
=(1/28)*(7x-3)^4
5)12*(-1/6) ∫ (4-6x)^(-5)d(4-6x)=(-2)*(4-6x)^(-4)/(-4)+C=
=(1/2)*(1/(4-6x)^4) + C
6)
∫ sin3xdx= ∫ sin3x*d(3x)/3=(1/3) ∫ sin(3x)d(3x)=(1/3)*(-cos3x)+C=
=(-1/3)cos3x+C
