Задача 33693 ...
Условие
1687. ∫ (2x⁻¹.² + 3x⁻⁰.³ - 5x⁰.³⁸) dx.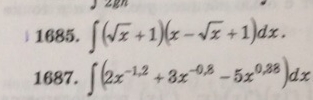
Решение
(sqrt(x)+1)*(x-sqrt(x)+1)=(sqrt(x))^(3) +1^(3)=x^(3/2)+1
∫ (x^(3/2)+1)dx=
Интеграл от суммы (разности) равен сумме (разности) интегралов
= ∫ (x^(3/2)dx+ ∫ dx=
по формуле
[b]∫ x^( α )dx=x^( α +1)/( α +1) + C [/b]
=x^((3/2)+1)/((3/2)+1) + x + C=
=x^(5/2)/(5/2) + x +C=
=(2/5)*x^(2)*sqrt(x)+x+C
1687
Интеграл от суммы (разности) равен сумме (разности) интегралов.
Постоянный множитель можно вынести за знак интеграла
=-2 ∫ x^(-1,2)dx+3 ∫ x^(-0,8)dx-5 ∫ x^(0,38)dx=
по формуле
[b]∫ x^( α )dx=x^( α +1)/( α +1) + C [/b]
=-2*x^(-1,2+1)/(-1,2+1) +3*x^(-0,8+1)/(-0,8+1) -5*x^(0,38+1)/(0,38+1)
+C=
=(10/x^(0,2)) +15x^(0,2)-(250/69)x^(1,38) +C
