Задача 33910 ...
Условие
∫ sin3xdx/sqrt(5+cos3x)
...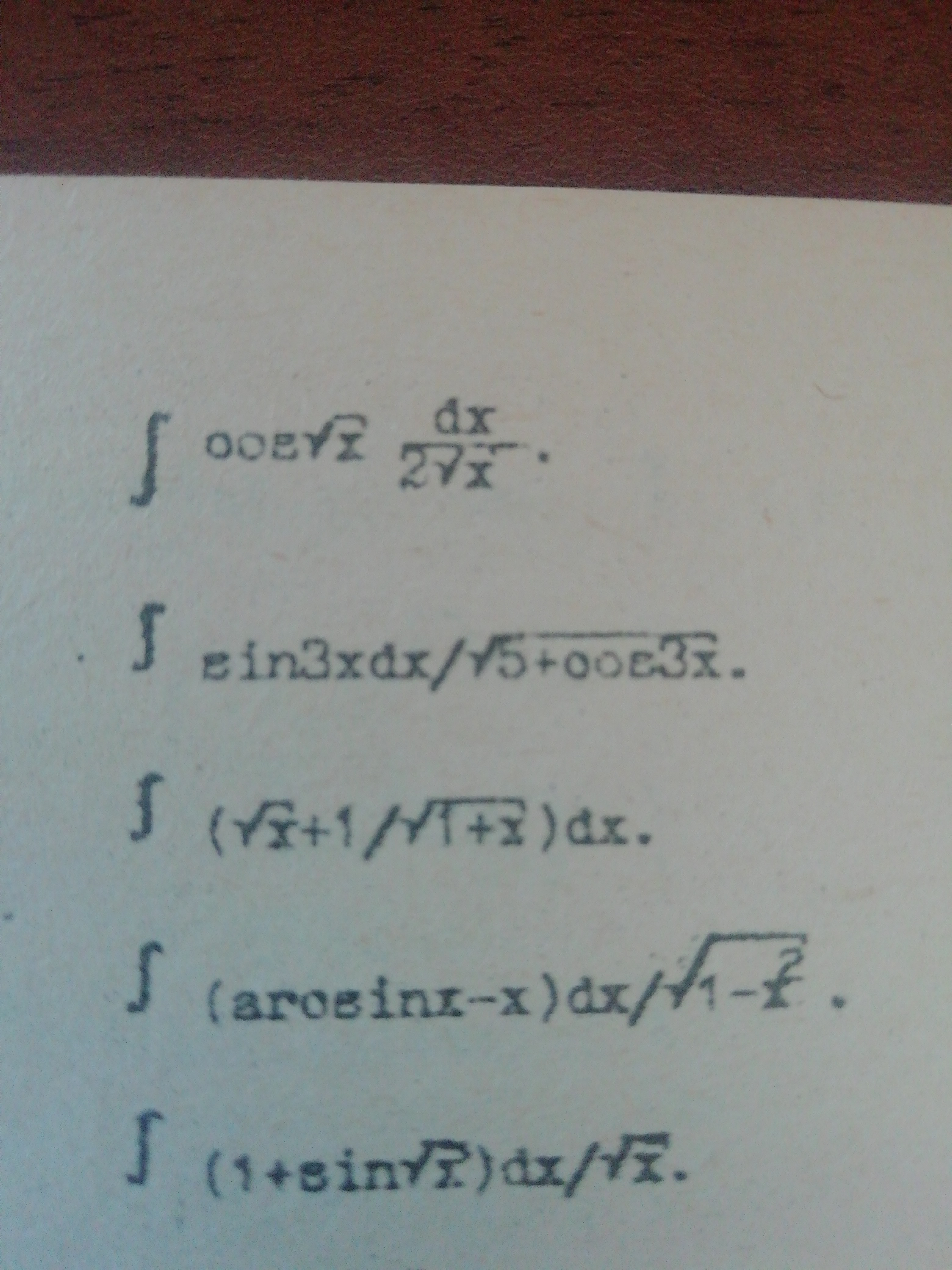
Решение
[b]Замена переменной
sqrt(x)=t
dt=dx/(2sqrt(x))[/b]
получаем табличный интеграл
∫ costdt=sint+C=sin(sqrt(x))+C
2.
[b]Замена переменной
5+cos3x=t[/b]
dt=(5+cos3x)`dx
dt=-sin3x*(3x)`dx
dt=-3sin3xdx
[b]sin3xdx=(-1/3)dt
[/b]
получаем табличный интеграл
∫ (-1/3)dt/sqrt(t)=(-1/3)2sqrt(t)+C=(-2/3)sqrt(5+cos3x)+C
3.
Интеграл от суммы( разности) интегралов равен сумме (разности) интегралов.
= ∫ sqrt(x)dx+ ∫ dx/sqrt(1+x)
Первый интеграл
∫ dx/sqrt(x)
табличный интеграл
=2sqrt(x)
Второй интеграл
∫ dx/sqrt(1+x)= [b][замена: sqrt(1+x)=t;1+x=t^2; x=t^2-1;dx=2tdt ][/b]
∫ 2tdt/sqrt(t)=2∫dt=2t=2sqrt(1+x)
О т в е т. ∫ sqrt(x)dx+ ∫ dx/sqrt(1+x)=2sqrt(x)+2sqrt(1+x)+C
4.
Интеграл от суммы( разности) интегралов равен сумме (разности) интегралов.
= ∫ arcsinxdx/sqrt(1-x^2) - ∫ xdx/sqrt(1-x^2)
Первый интеграл
∫ arcsinxdx/sqrt(1-x^2) [b][ замена: arcsinx=t; dt=dx/sqrt(1-x^2)]=[/b]
получаем табличный интеграл
∫ tdt=t^2/2=(arcsinx)^2/2
Второй интеграл
∫ xdx/sqrt(1-x^2)= [b][ замена: 1-x^2=u; du=-2xdx⇒xdx=(-1/2)du][/b]
получаем табличный интеграл
∫ (-1/2)du/sqrt(u)=(-1/2)*2sqrt(u)=-sqrt(1-x^2)
О т в е т. ∫ arcsinxdx/sqrt(1-x^2) - ∫ xdx/sqrt(1-x^2)=
=(arcsinx)^2/2-sqrt(1-x^2) +C
5.
Интеграл от суммы( разности) интегралов равен сумме (разности) интегралов.
= ∫ dx/sqrt(x) + ∫ sin(sqrt(x))dx/sqrt(x)
Первый интеграл
∫ dx/sqrt(x)
табличный интеграл
=2sqrt(x)
Второй интеграл
∫ sin(sqrt(x))dx/sqrt(x)= [b][замена: sqrt(x)=t;dt=dx/(2sqrt(x)); dx/(sqrt(x))=2dt; ][/b]
получаем табличный интеграл
∫ 2sintdx=2*(-cost)=-2cos(sqrt(x))
О т в е т. ∫ dx/sqrt(x) + ∫ sin(sqrt(x))dx/sqrt(x)=2sqrt(x)-2cos(sqrt(x))+C
