Двойные интегралы

1. Вычислить интеграл: [m]\int_{0}^{1}dx\int_{0}^{1}\frac{x^{2}dy}{1+y^2}[/m]
2. Изменить порядок интегрирования в повторном интеграле: [m]\int_{-1}^{1}dx\int_{-\sqrt{1-x^2}}^{1-x^2}f(x; y)dy[/m]

1. Найти уравнения линий, ограничивающих область интегрирования
интеграла: [m]\int_{0}^{2}dx\int_{\sqrt{2x-x^2}}^{\sqrt{2x}}f(x; y)dy[/m]
2. С помощью тройного интеграла вычислить объем тела,
что ограничено поверхностями: [m](x-1)^2+y^2=z; 2x+z=2[/m]

Вычислить площадь области

∫∫_D (12xy+9x²y²) dxdy
D: ...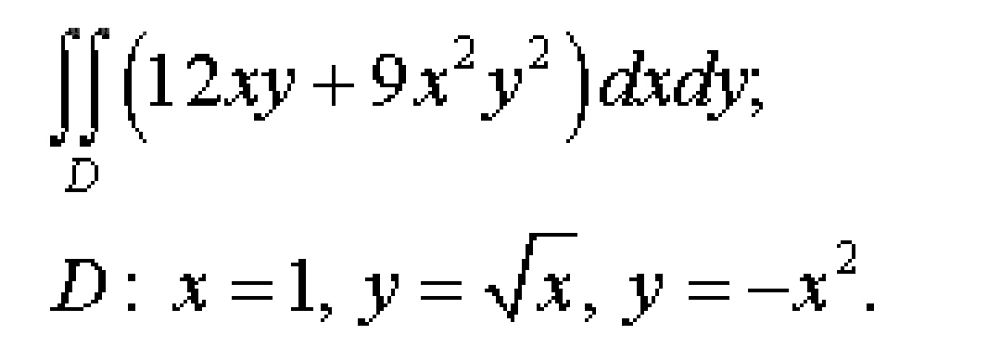

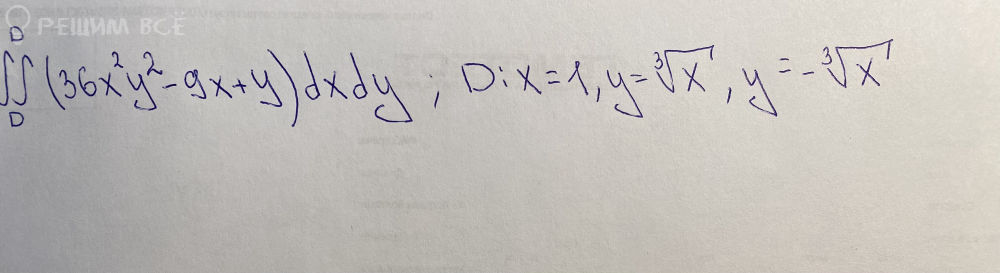
Вычислить двойной интеграл по области D, ограниченной указанными линиями. Сделать чертеж области D.

Найти объем тела ограниченного поверхностями:
x² + y² = 50, x = √5y, x = 0, z = 6y/11.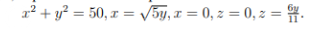

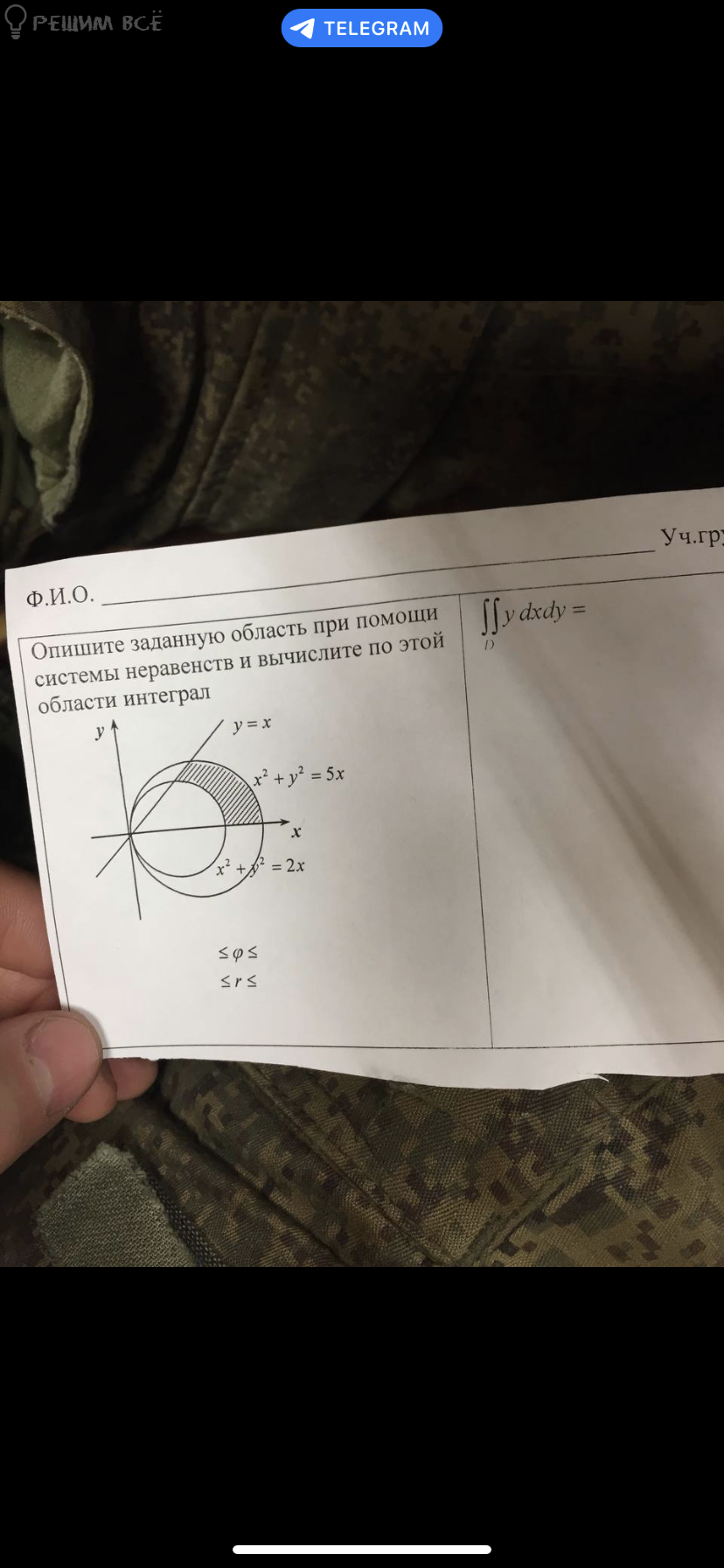
Опишите заданную область при помощи системы неравенств и вычислите по этой области интеграл

с помощью тройного интеграла найти объём тела, ограниченного цилиндром x²+y²=y конуса z=√x²+y^y и плоскостью z=0

Найти координаты центра тяжести фигуры, ограниченной следующими
линиями y=–x2+4x+3; 3x–4y–5=0

x^{2}+y^{2}=5;z=x^{2}+y^{2} вычислить объем тела ограниченного данными поверхностями и расположенного в первом октанте

Вычислить объем тела, ограниченного поверхностями: bz=x²+y²; z=0; x²+y²=2bx

Необходимо найти объем фигуры ограниченной x² + y² = R² и z = x³ / a² и плоскостью z=0. (ответ приложен)

Найти объём тела, ограниченного поверхностями
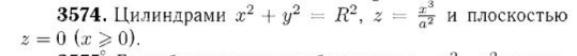
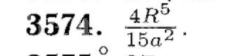
y=16√2x, y=√2x, z=0, z+x=2

Вычислить интеграл В ответе введите число, округлив его до целых (например, если в ответе у вас получилось л, то введите 3). Ответ:

Вычислить объем тела, ограниченного данными поверхностями:
z = 0; z = 4 – x²; y = 0; x + y = 6.

Вычислить с помощью двойного интеграла в полярных координатах
площадь фигуры, ограниченной линиями x2+y2–4x=0 x≥2