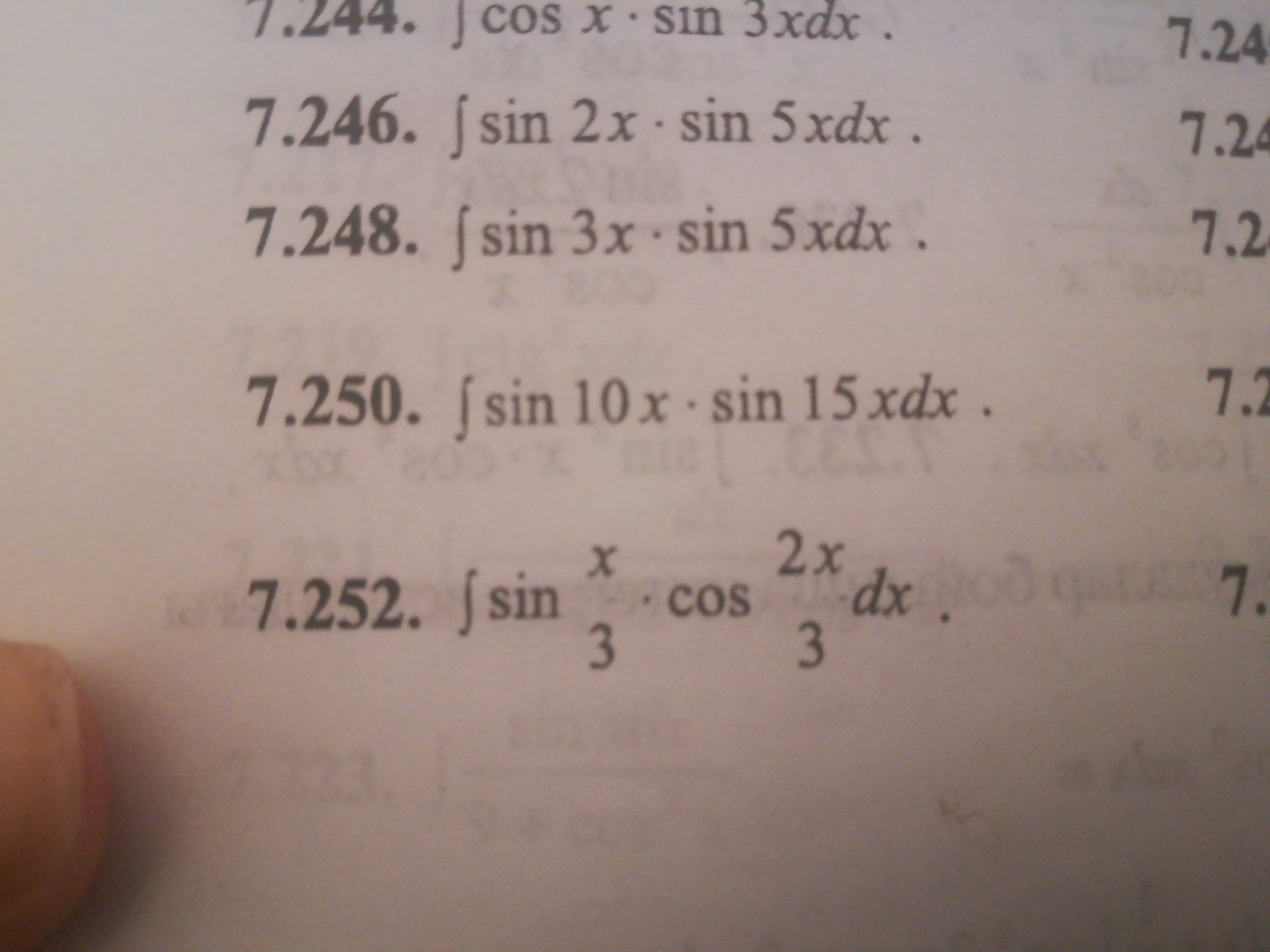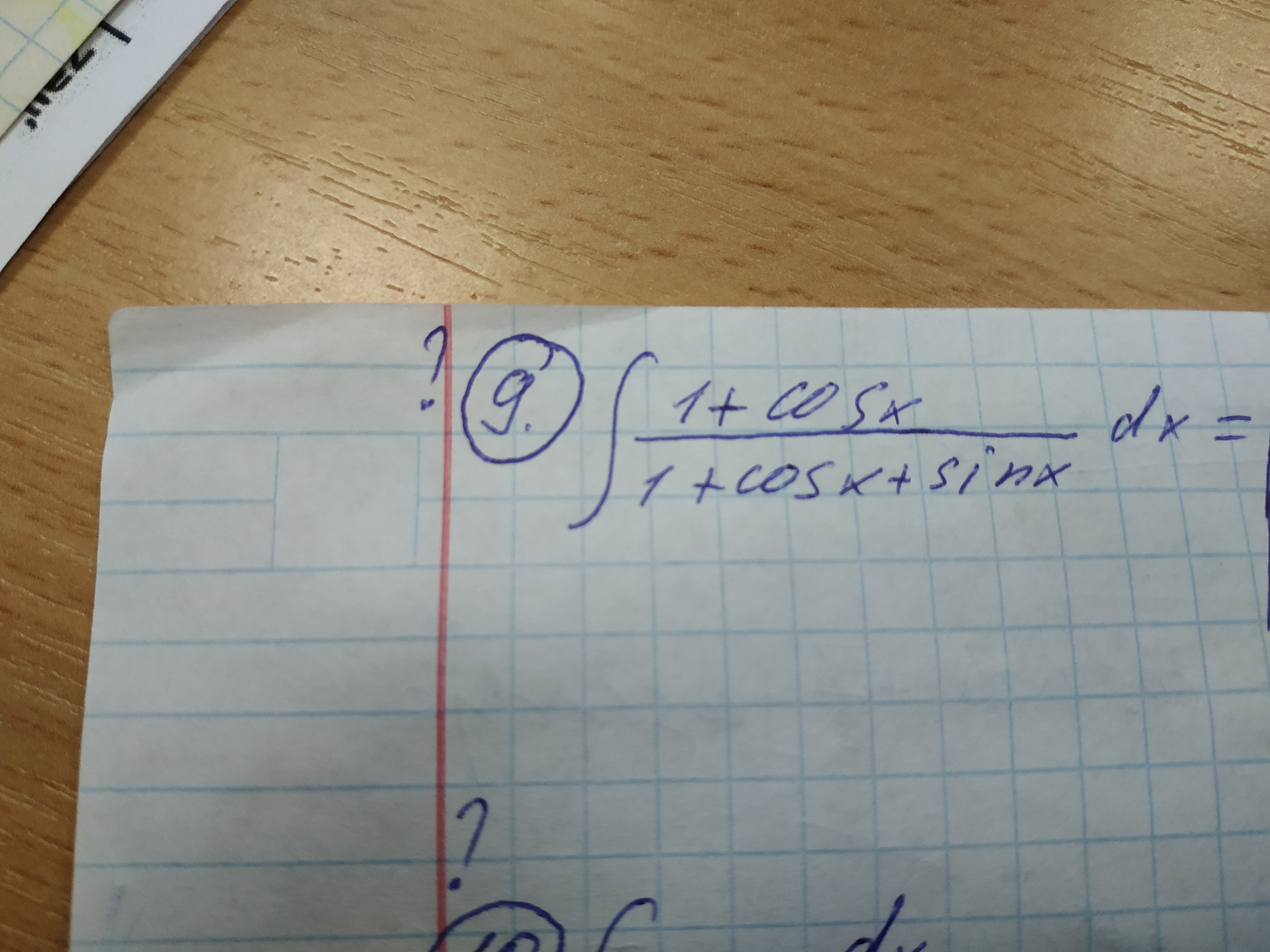Интегрирование тригонометрических функций
Практика (38)
[block] ∫ (dx)/(4cosx+sinx)[/block]
∫ cos^7 x · dx ,

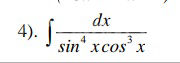
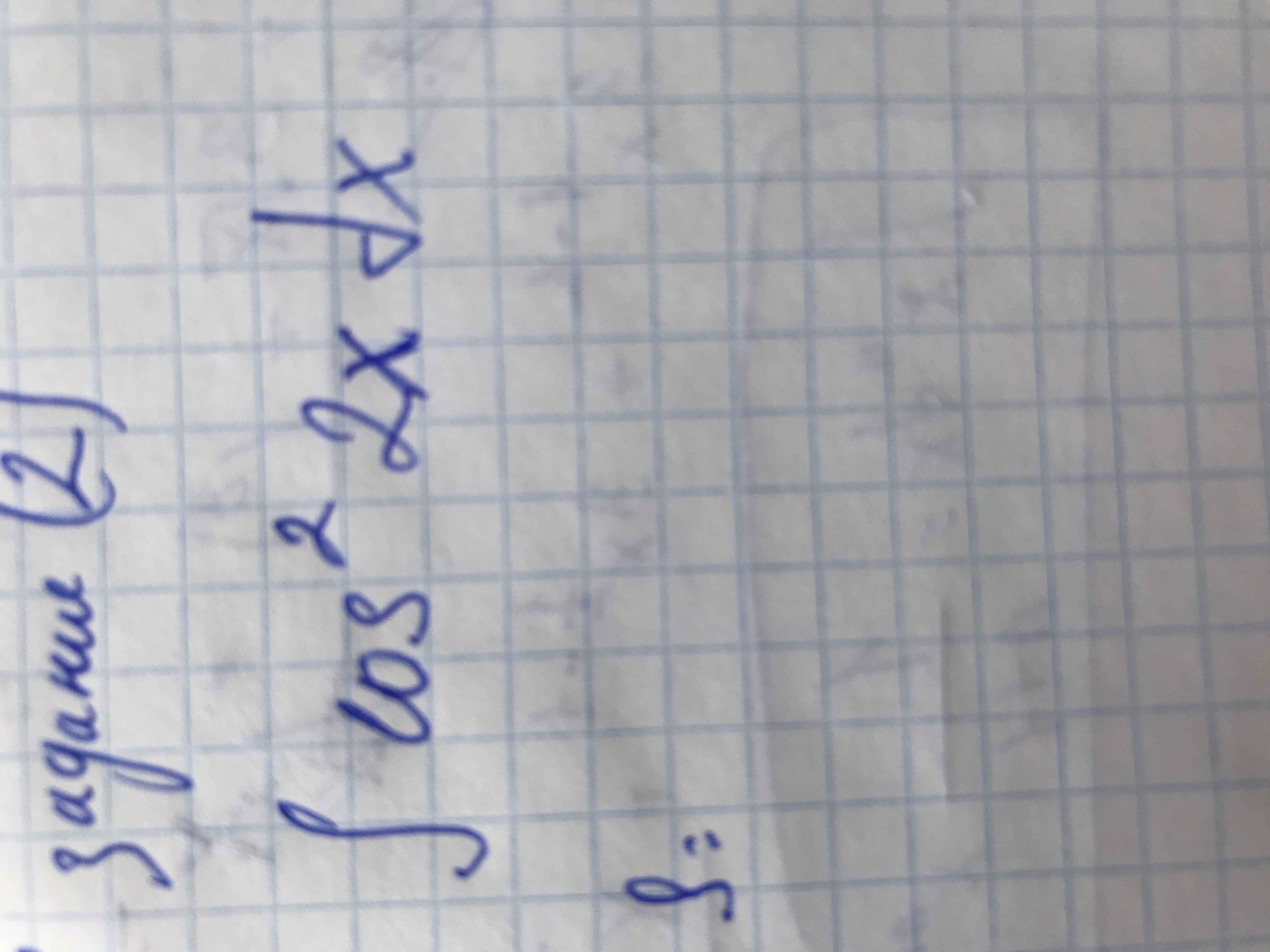
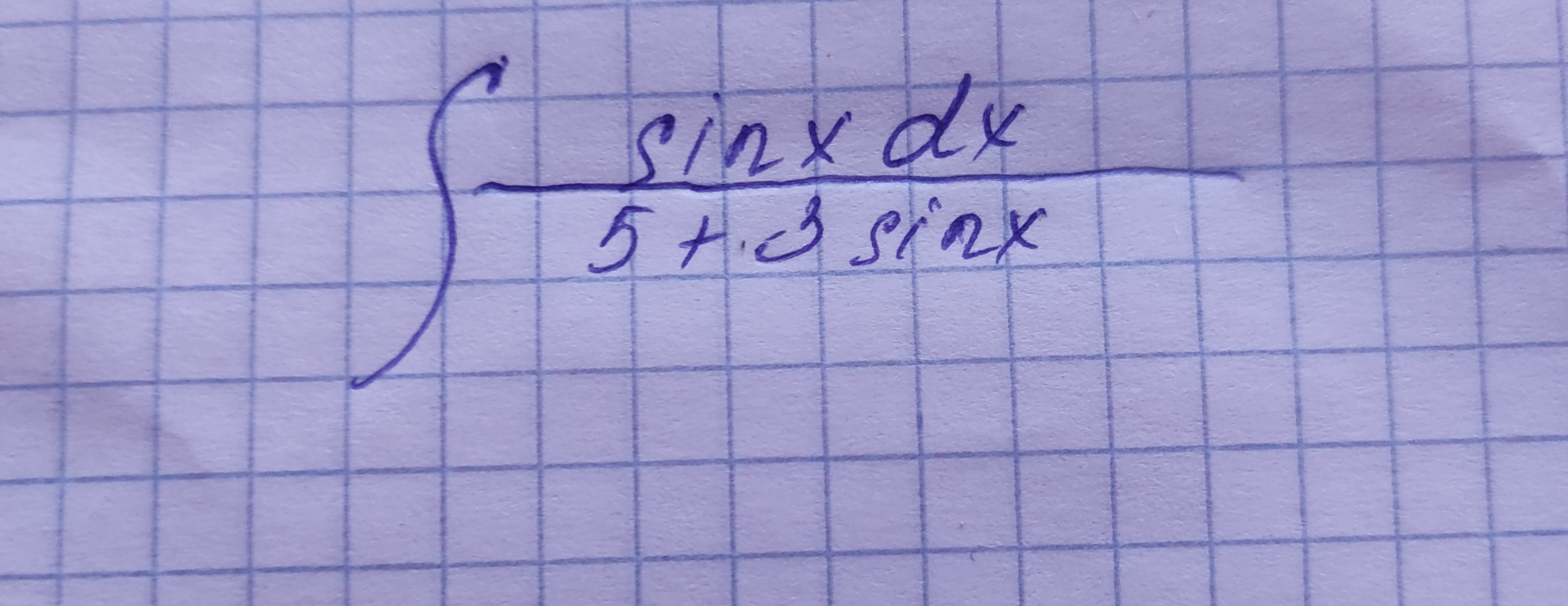
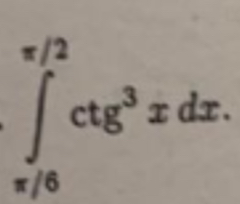
Найти неопределенный интеграл. (подсказка ctg2x = cos2x / sin 2x).
u = sin 2x, du = 2cos2xdx, dx = du/2cos2x, подставьте в интеграл
∫sin^2(3x/2)dx
sin α cos β = (sin (α + β) + sin (α - β)) / 2
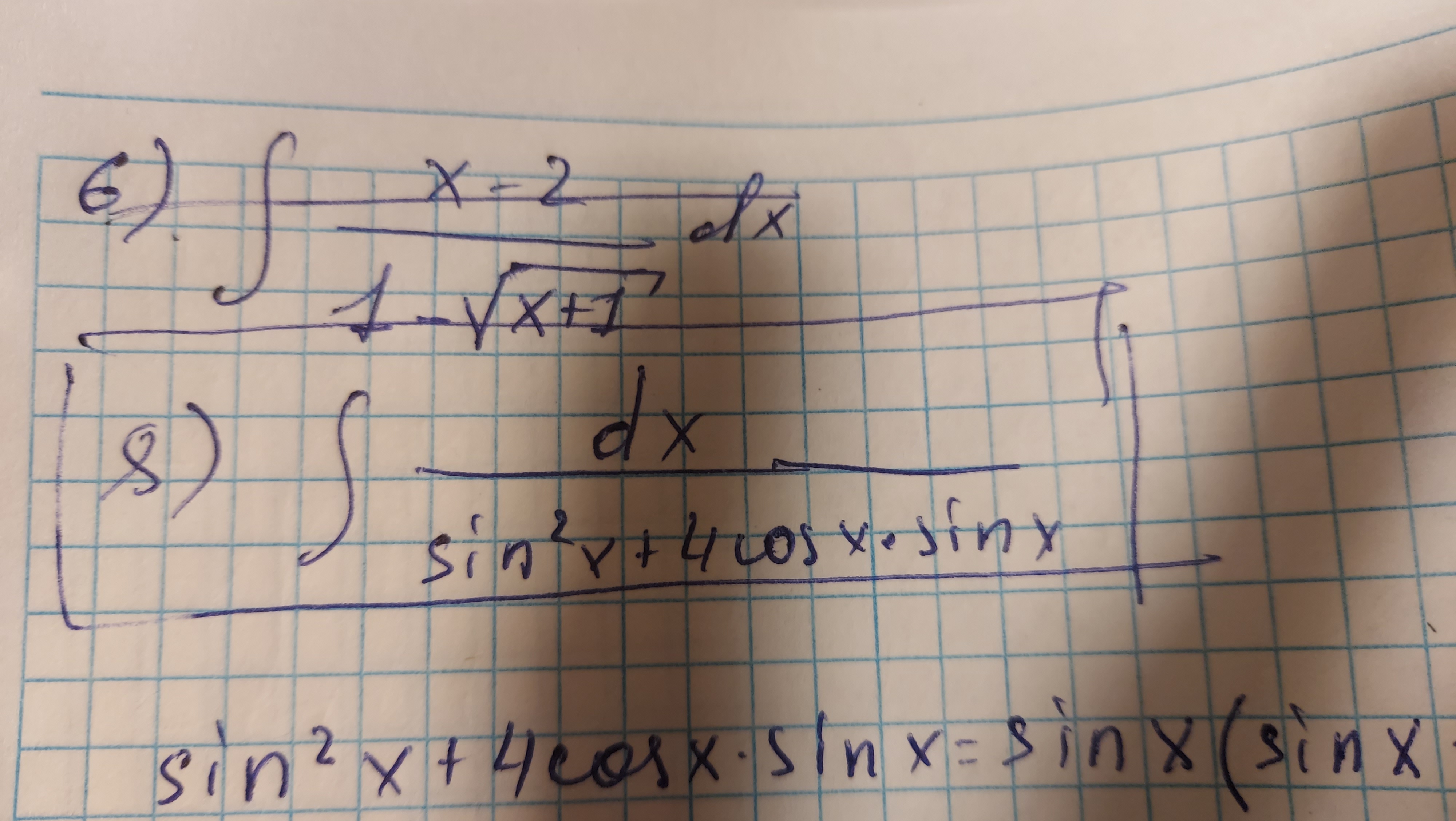

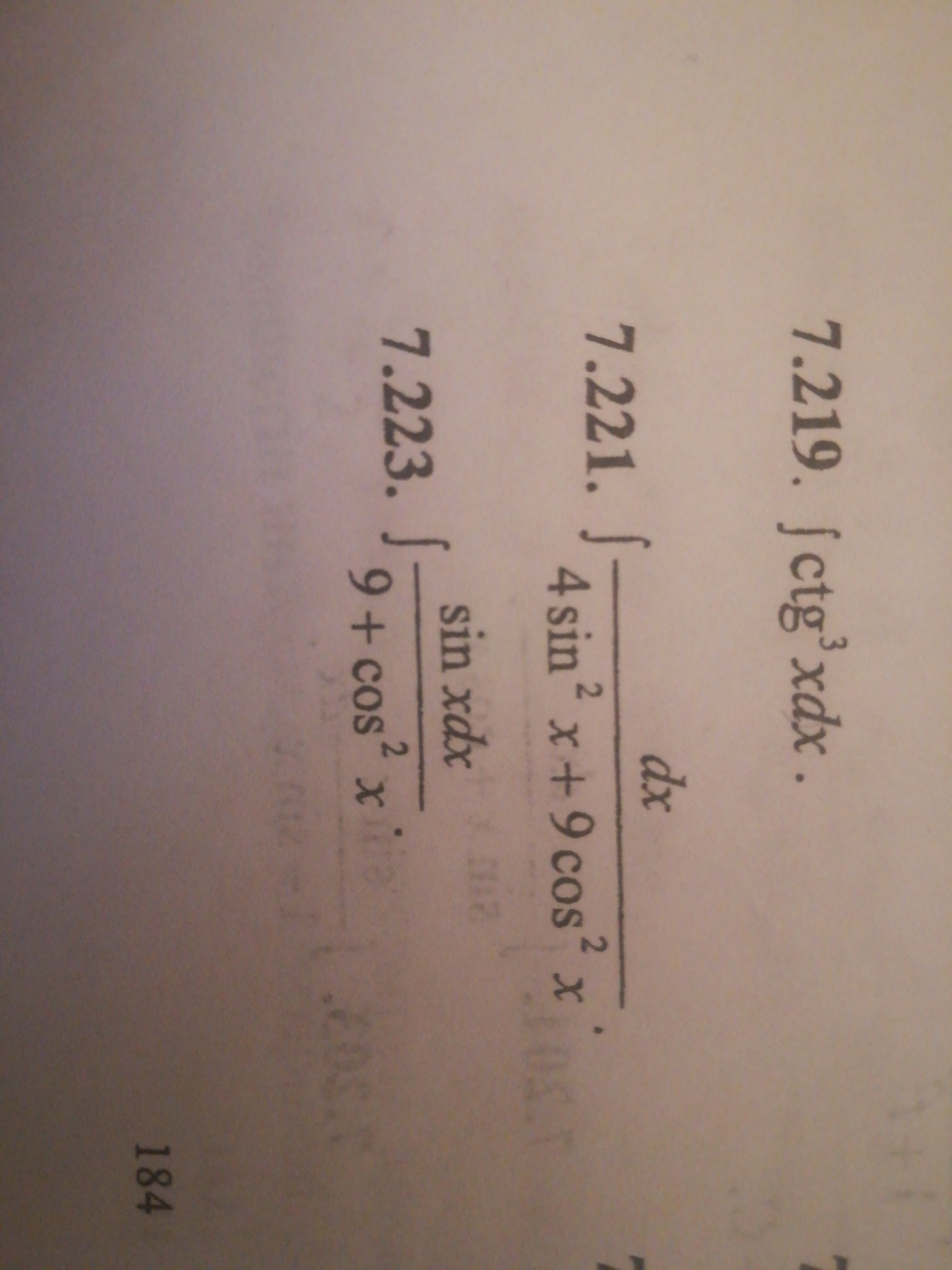
∫cos²8xdx
если можно подробное решение
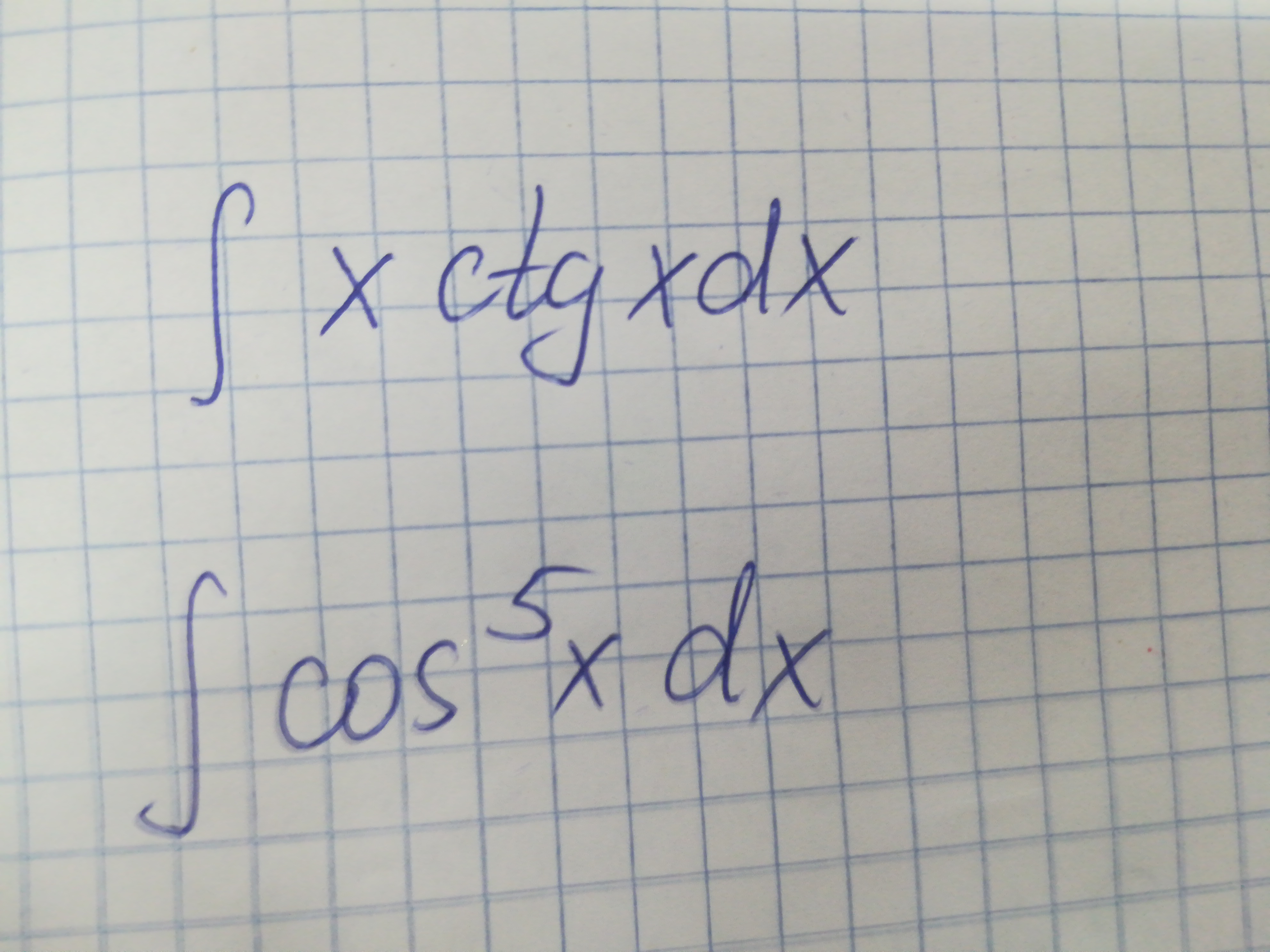
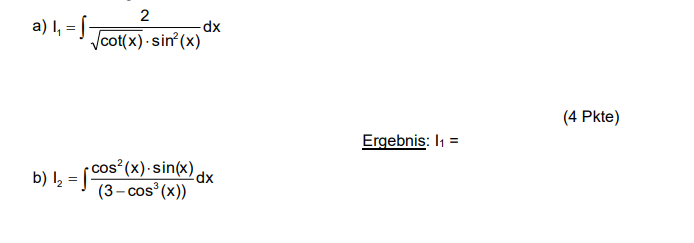

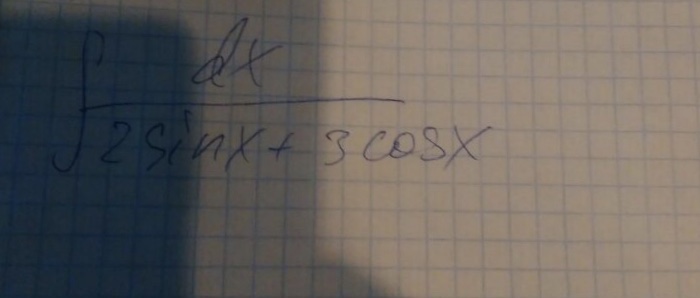
∫ cos^5 x / (1 + sin x) dx;
∫ dx / (2 sin^2x + 7 cos^2x);
∫ sin^2 x / cos^(10) x dx;
∫ sin^4 x cos^3 x dx;
∫ sin^6 2x dx;
∫ cos 3x cos 2x dx
∫ sin^4x×cos^4x dx
∫ tg^4 x/2 dx
подробное решение
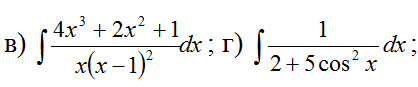
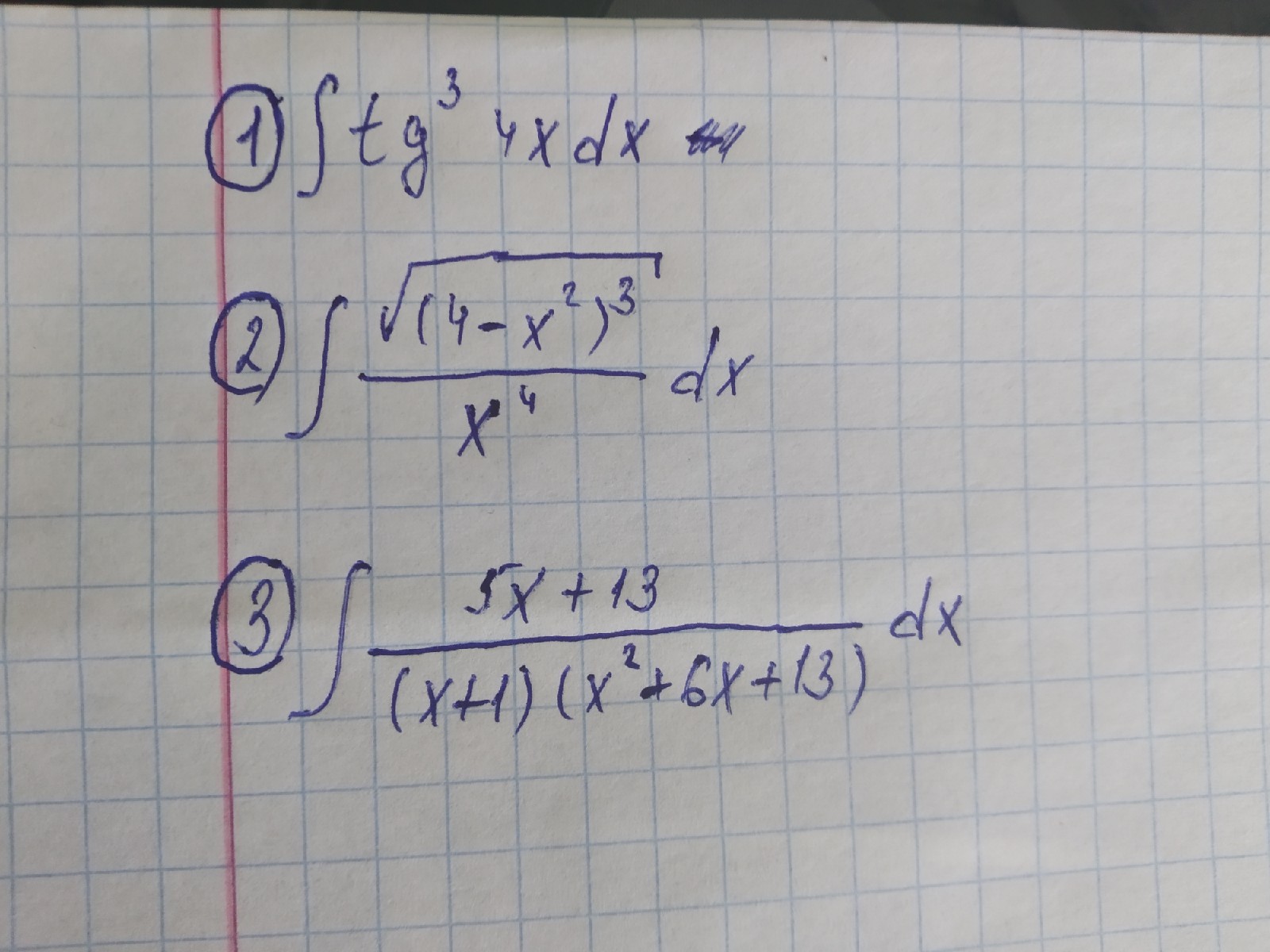
14. ∫ 2cos^4y dy
16. ∫ dx / cos^3(x/4)
17. ∫ ctg^(3) (2/3) x dx
а) ∫(корень 3ей степени(1+корень 4ой степени(x))/sqrt(x) dx б) ∫ tg^5xdx. Смотреть фото. Можно с подробностями или с объяснением, пожалуйста. 
2.Вычислите указанный определенный интеграл, используя
формулу Ньютона–Лейбница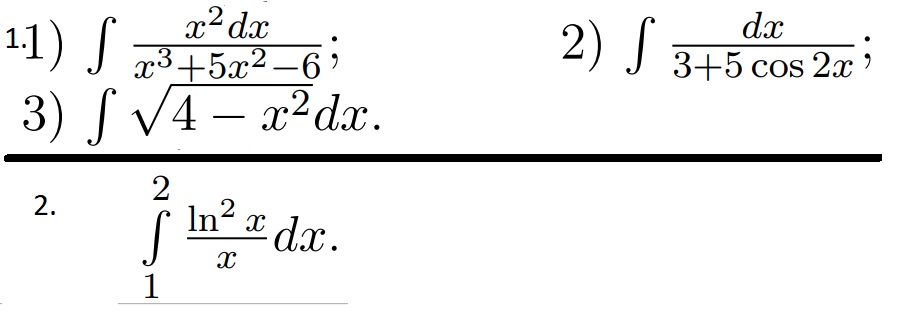
Навигация
- Непосредственное интегрирование
- Метод замены переменной
- Интегрирование по частям
- Интегрирование рациональных дробей
- Интегрирование некоторых иррациональностей
- Интегрирование тригонометрических функций
- Определенный интеграл и его приложения
- Криволинейный интеграл
- Двойные интегралы
- Задачи теоретического характера
- Пространства Метрика