Задача 61627 Интеграл 1/((sin(x))^4(cos(x)^3))...
Условие
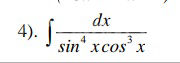
Решение
[m] ∫ \frac{dx}{sin^4xcos^3x}= ∫ \frac{cosxdx}{sin^4xcos^4x}dx=[/m]
Подстановка
[m]sinx=t[/m] ⇒ sin^2x=t^2 ⇒ cos^2x=1-sin^2x=1-t^2
[m]cosx dx=dt[/m]
[m]= ∫ \frac{dt}{t^4(1-t^2)^2}=[/m] - интегрирование рац дробей
Раскладываем дробь на простейшие
Применяем "искусственный прием" -t^2 и + t^2:
[m]= \frac{1}{t^4(1-t^2)^2}= \frac{1-t^2+t^2}{t^4(1-t^2)^2}=\frac{1-t^2}{t^4(1-t^2)^2}+\frac{t^2}{t^4(1-t^2)^2}= [/m]
[m]=\frac{1}{t^4(1-t^2)}+\frac{1}{t^2(1-t^2)^2}= [/m]
[m]=\frac{1-t^2+t^2}{t^4(1-t^2)}+\frac{1-t^2+t^2}{t^2(1-t^2)^2}=\frac{1-t^2}{t^4(1-t^2)}+\frac{t^2}{t^4(1-t^2)}+\frac{1-t^2}{t^2(1-t^2)^2}+\frac{t^2}{t^2(1-t^2)^2}= [/m]
[m]=\frac{1}{t^4}+\frac{1}{t^2(1-t^2)}+\frac{1}{t^2(1-t^2)}+\frac{1}{(1-t^2)^2}= [/m]
