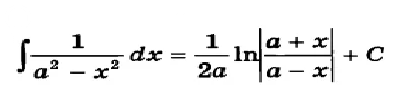Задача 63090 Интегрирование иррациональных функций....
Условие

Решение
В каждом интеграле отдельный метод интегрирования
1) выделение полного квадрата и сведение к табличному
2) замена переменной.
[b]Универсальная подстановка [/b] применяется для вычисления интеграла
3)[m] ∫ \frac{dx}{4cosx+sinx}[/m]
(см скрин 1)
Тогда интеграл принимает вид:
[m] ∫ \frac{\frac{2dt}{1+t^2}}{4\cdot \frac{1-t^2}{1+t^2}+\frac{2t}{1+t^2}}= ∫\frac{2dt}{4-4t^2+2t}=∫\frac{dt}{2-2t^2+t} [/m]
Получили интеграл, содержащий квадратный трехчлен.
Выделяем полный квадрат
[m]2-2t^2+t=-2(t^2-\frac{1}{2}t-1)=-2(t^2-2\cdot \frac{1}{4}+(\frac{1}{4})^2-(\frac{1}{4})^2-1)=[/m]
[m]=-2\cdot ((t-\frac{1}{4})^2-\frac{17}{16})=2(\frac{17}{16}-(t-\frac{1}{4})^2)[/m]
[m]∫\frac{dt}{2-2t^2+t}= \frac{1}{2}∫\frac{dt}{\frac{17}{16}-(t-\frac{1}{4})^2} [/m]
Табличный интеграл ( см. скрин 2)
[m] a^2=\frac{17}{16} [/m] ;
[m]x=t-\frac{1}{4}[/m]
[m]= \frac{1}{2}\cdot \frac{1}{2\frac{\sqrt{17}}{4}}ln|\frac{\frac{\sqrt{17}}{4}-(t-\frac{1}{4})}{\frac{\sqrt{17}}{4}+(t-\frac{1}{4})}| + C[/m]
где
t= tg (x/2)
можно упростить...
[m]= \frac{1}{\sqrt{17}}ln|\frac{\sqrt{17}+1-4tg\frac{x}{2}}{\sqrt{17}-1+4tg \frac{x}{2}}| + C[/m] - это ответ
4) 5) интегрирование тригонометрических функций.
Каждый интеграл решается отдельным приемом ( методом). которые нужно знать.
Если хотите получить подробные решения по каждому интегралу выставляйте один интеграл в вопросе.
В решении привожу формулы, которые требуются для решения задачи. Все рисунки прикрепляются отдельно и потому очень трудно понять какой скрин к какому интегралу относится. Так что не поленитесь и задайте каждый вопрос отдельно...