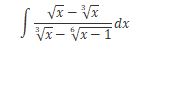Интегрирование некоторых иррациональностей
Практика (30)
∫ sqrt(3-2x-x^2) dx , x+1 = 2sint
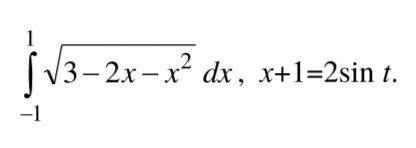

неопределенный интеграл
(√х) / (x-3√x) dx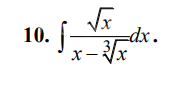
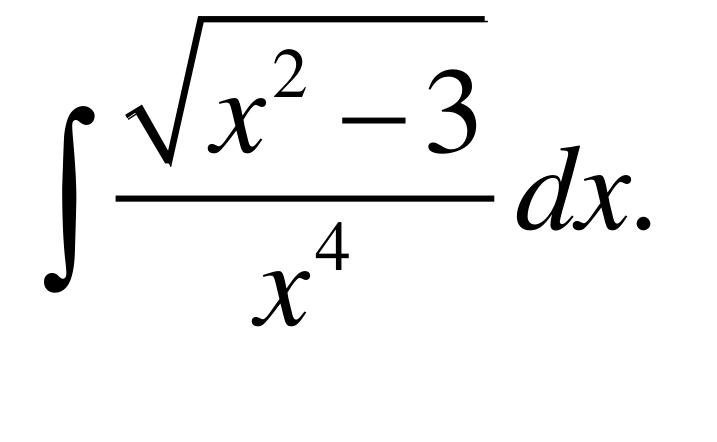
∫ √x + x / √x - 2 dx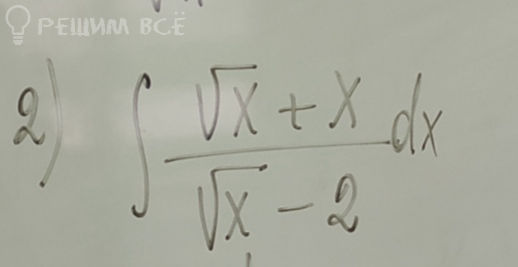
1) ∫ dx / sqrt(x² - 4x + 5)
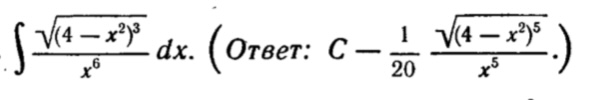
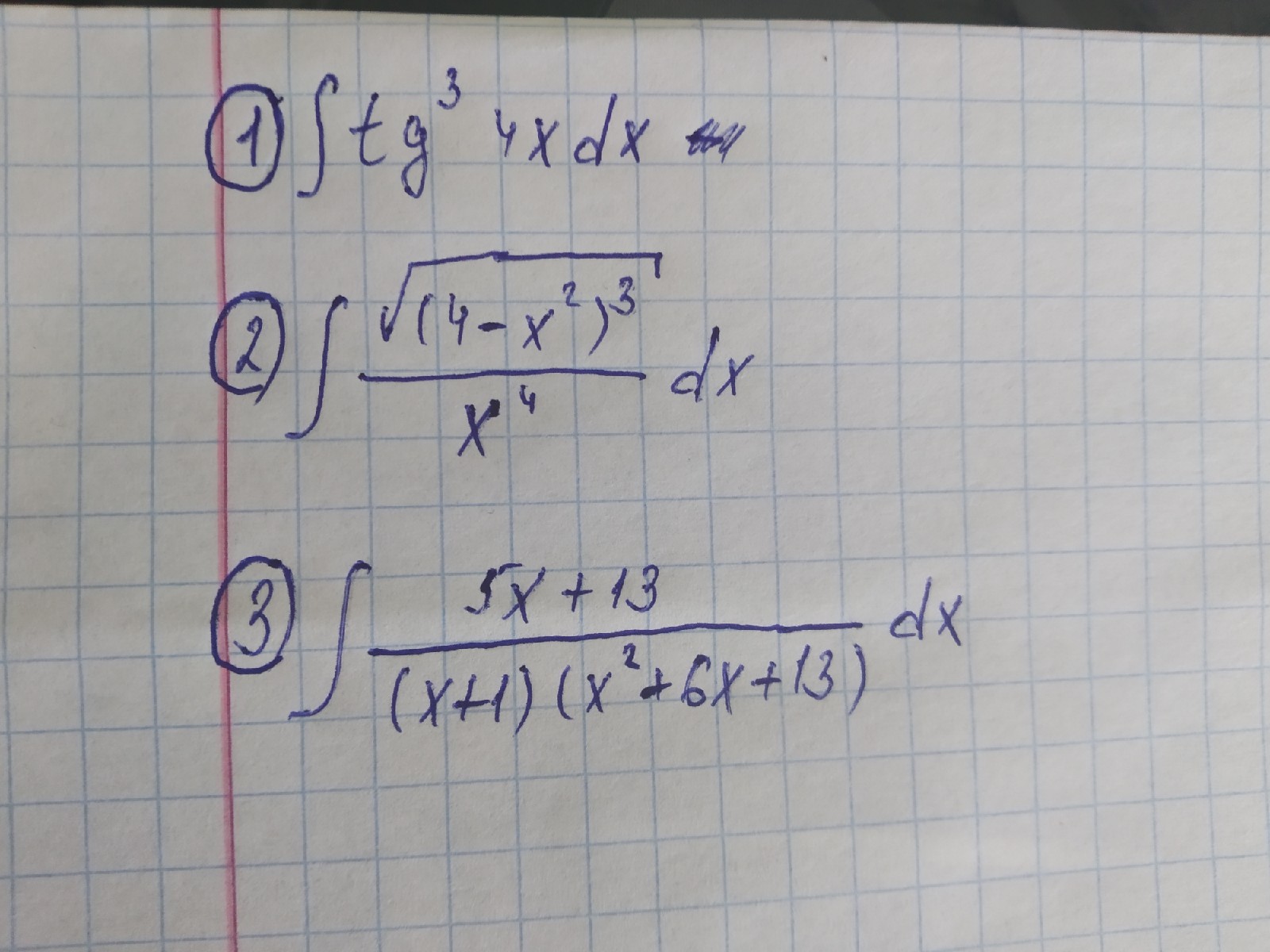
а) ∫(корень 3ей степени(1+корень 4ой степени(x))/sqrt(x) dx б) ∫ tg^5xdx. Смотреть фото. Можно с подробностями или с объяснением, пожалуйста. 
269. ∫√(1 - 4x - x²)dx .
59. ∫ dx / √ ( x + 1 + √(x + 1)³)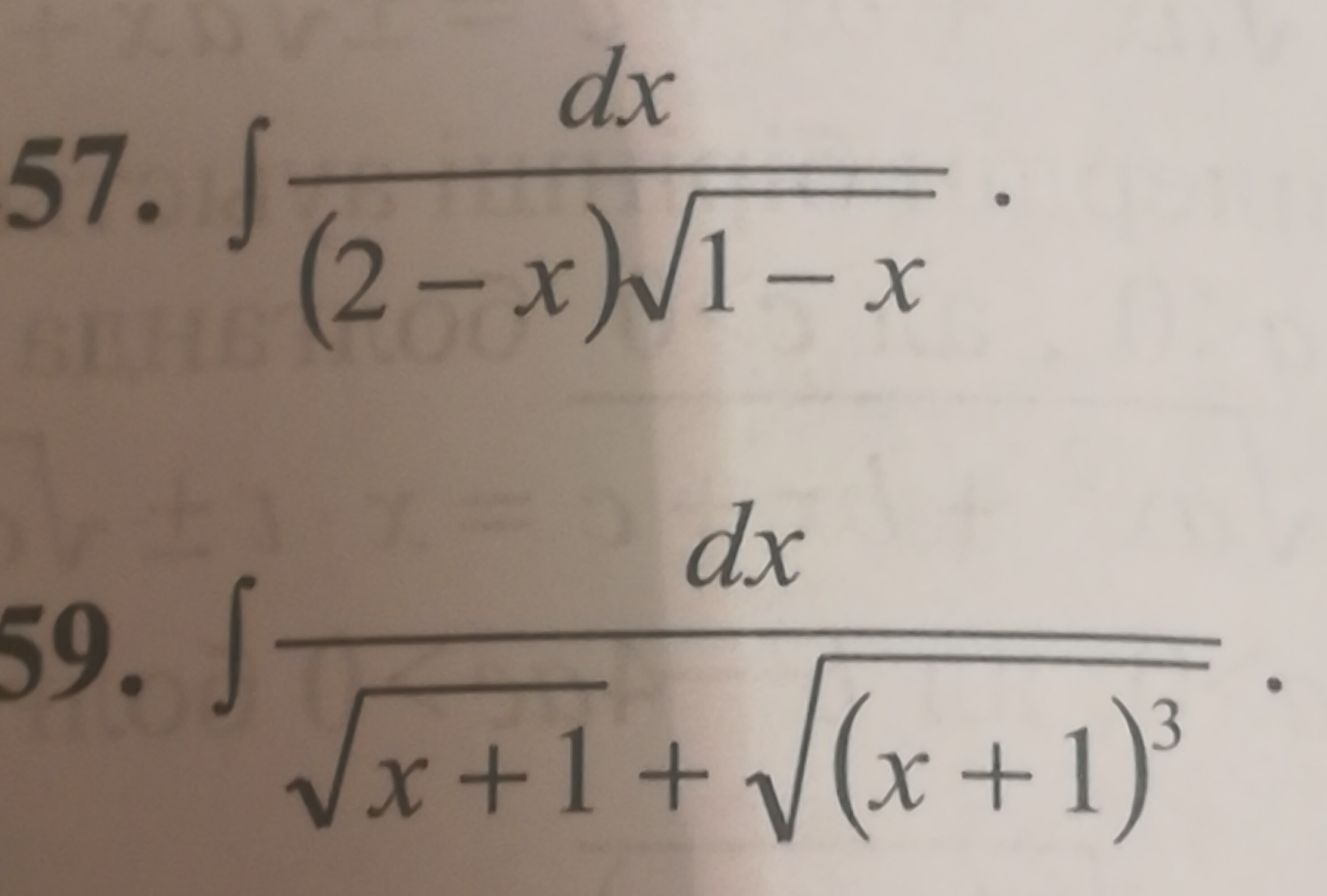
dx/ sqrt(x^2+8x+9)
Помогите решить.
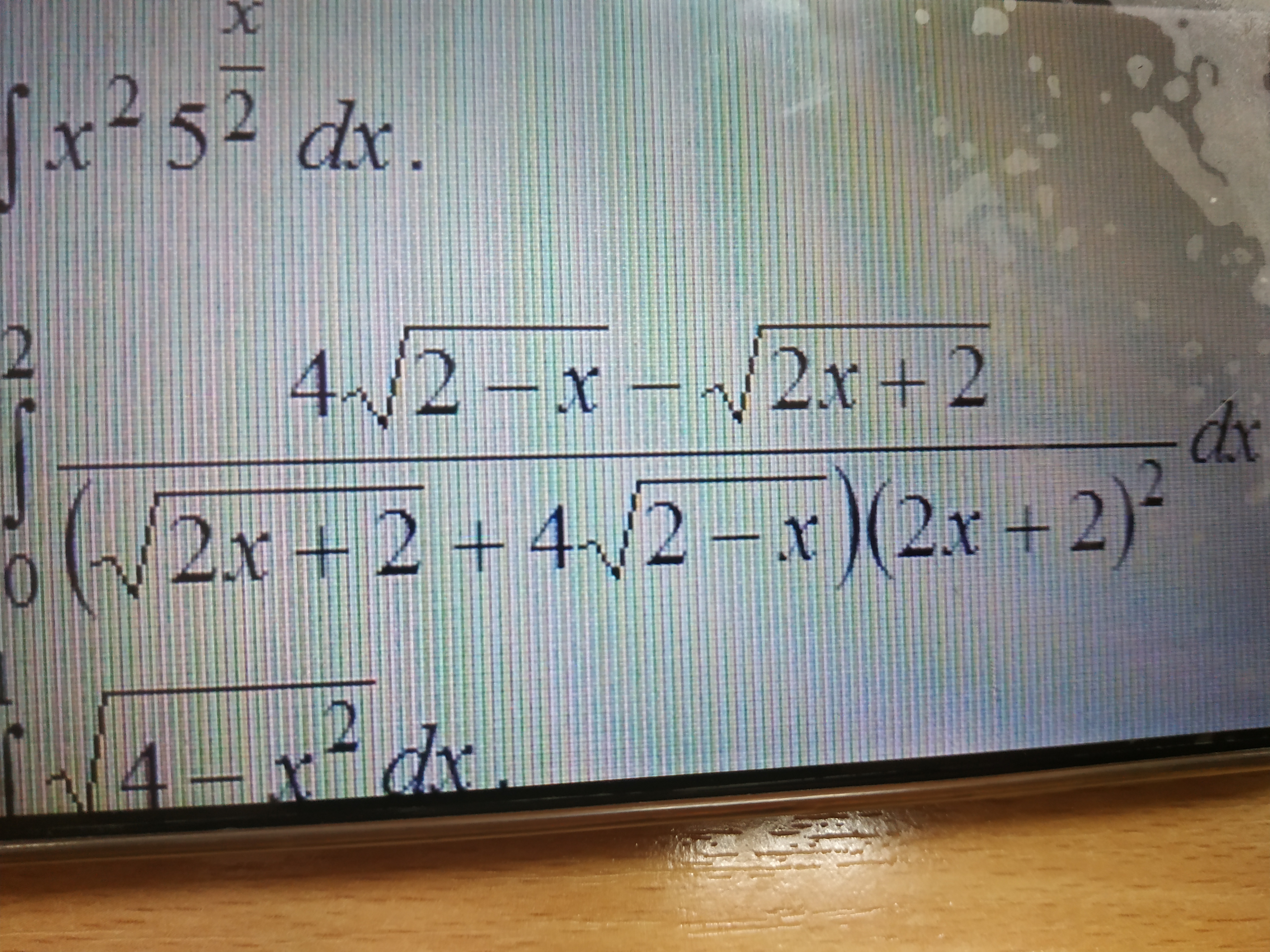
∫ dx / ((2x + 1)^2 - √(2x + 1))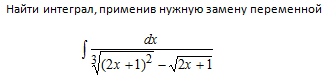
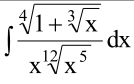
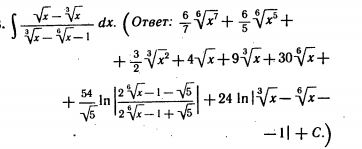
подробное решение
∫(from 1 to 16) (dx / (x + √(4)x))
в) ∫(4x^3 + 2x^2 + 1) / x(x - 1)^2 dx ; Г) ∫(1 / (2 + 5cos^2x)) dx ; Д)
∫(4x + 3) / √(7 - 2x - x^2) dx.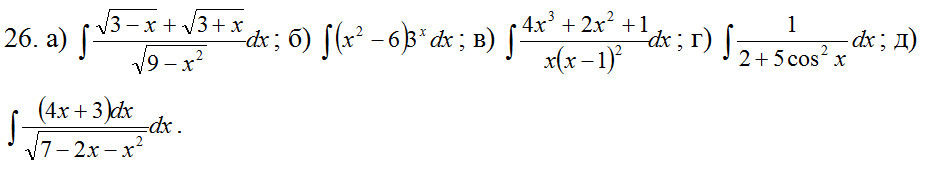
2.Вычислите указанный определенный интеграл, используя
формулу Ньютона–Лейбница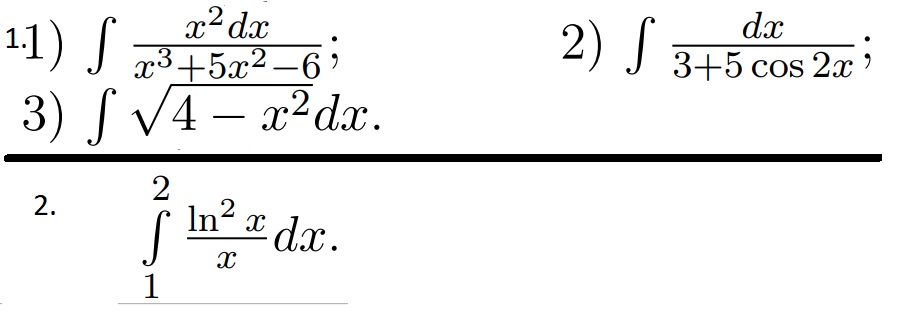
Навигация
- Непосредственное интегрирование
- Метод замены переменной
- Интегрирование по частям
- Интегрирование рациональных дробей
- Интегрирование некоторых иррациональностей
- Интегрирование тригонометрических функций
- Определенный интеграл и его приложения
- Криволинейный интеграл
- Двойные интегралы
- Задачи теоретического характера
- Пространства Метрика