Задача 31817 ...
Условие
59. ∫ dx / √ ( x + 1 + √(x + 1)³)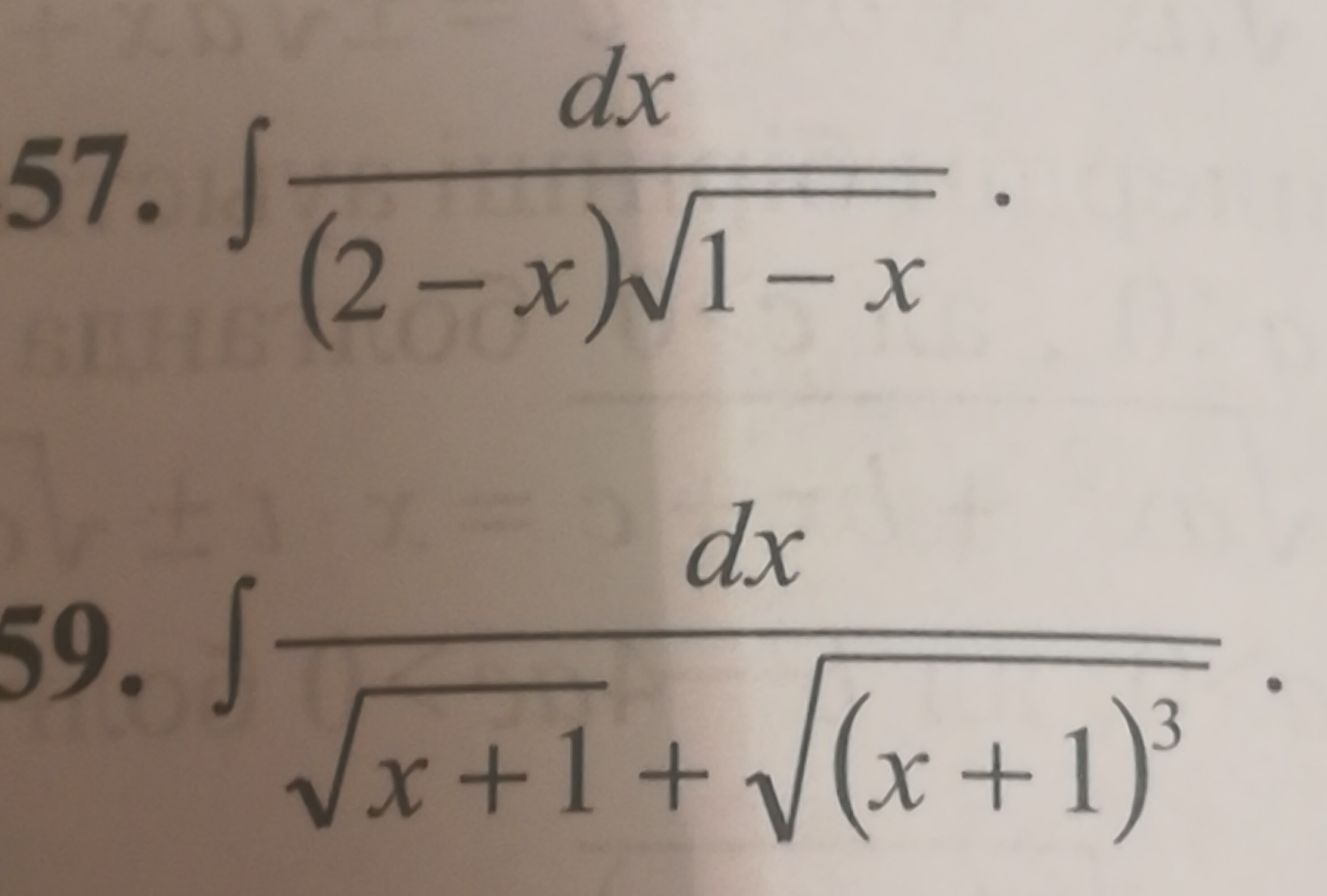
предмет не задан
956
Решение
★
sqrt(1-x)=t
1-x=t^2
x=1-t^2
2-x=1+t^2
dx=-2tdt
= ∫ (-2tdt)/((1+t^2)*t)=-2 ∫ dt/(1+t^2)=-2arctgt+C=
=-2arctgsqrt(x-1) + C
59
sqrt(x+1)=t
sqrt((x+1)^3)=t^3
x+1=t^2
x=t^2-1
dx=2tdt
= ∫ 2tdt/(t+t^3)=2 ∫ dt/(1+t^2)=2arctg(t) + C= 2 arctgsqrt(x+1) + C

